【中学・高校物理】浮力に関する直感的な解釈
浮力の説明の時に、物体の下面の圧力のほうが上面の圧力より大きいから上向きに力が働き、それが浮力であると説明されますが、聡明な人ほど、ピンとこないはず。
また、どうして浮力の大きさが、押しのけた体積分の、媒質の重さに等しいかも、説明されないことが多い。
ここでは、浮力に関する、直感的な解釈をしていきます。
まず、
浮力そのものとはどんなものか。
浮力というのをまず、説明してしまうと、例えば水の中にある形の物体があったとします。そのとき、物体の下の水分子は、物体の上の水分子よりも深い位置にあるわけで、それゆえ物体の上の水よりも圧迫されており、下の水分子たちはその分上よりも激しく動いているため、下の激しい動きの分子によって物体が上に押されます。それが浮力です。
さて、
浮力とは、物体の下部と下部での媒質の圧力の差から生まれる力、です。
でも、物体の下の方が、物体の上より、媒質(つまり水中だったら水)から受ける圧力が高いから、浮力が発生する、というけれど、
圧力っていう言葉自体、はっきりと理解できなかったりします。
圧力とは、「水分子や空気分子の、動きの激しさ」です。
物体の下の方の分子が、上に積もった分子に圧迫されているために、分子が激しく動いているから、物体は上向きに押し上げられる力「浮力」を受けるのです。
浮力に関して、ヘリウムの入っている(ゴム)風船を考えてみます。ゴム風船自体の重さはこれ以降言及されませんが、無視して考えていいです。ヘリウムは空気より軽い。
ここでも簡単に説明してしまうと、風船の中に空気が入っていたとしたら、浮力と重力が同じ状態:[ 浮力 \( = \) 重力 ] になっており、風船は上昇も下降もしませんが、風船の中にヘリウムが入っていると、ヘリウムは空気より軽いから、浮力が重力よりも勝り:[ 浮力 \( \gt \) 重力 ] 、風船は上昇するのです。
さて風船があって、まわりに空気が取り囲んでいるわけです。空気は、空気の分子、つまり酸素や窒素などの分子で構成されています。分子のレベルで考えれば、風船にたいして、四方八方から、ちいさなツブツブの空気分子が、すごい速さで、風船に当たっては、跳ね返っている。空気分子が風船に当たって跳ね返るときに、風船が力を受けますね。そして、風船の表面では、多数の空気分子が風船にぶつかっていますが、その単位面積にぶつかる全分子が風船に及ぼす力が、圧力です。単位面積あたりの力である圧力を、力の方向も考慮して(ベクトルとして)、風船の表面積全部で合計すれば、風船に働く全分子の及ぼす力ですし、先に言えば、この全部の力が、浮力となります。
ちなみに、空気分子はとても弾力性があるので、風船のゴムにダメージをあたえることなく、しなやかに跳ね返っていきます。とても小さな完璧な弾力性のボールが、風船に当たっては速度を失わず跳ね返されているイメージです。
そんなふうに考えていって、今度は、空気は、すごく我々の頭上何千メートル以上も上までありますが、地上の我々の手元にある風船のまわりにある空気なんて、風船の上部も下部も、差のない空気なんだと感じます。風船の上でも下でも、激しく動いている空気分子の動きにも、大差なんかない、風船が30cmの大きさだとしたら、風船の上と下で30cm の差しかない。風船の上と下で運動の激しさに差のない空気が、四方からまんべんなく、風船の周りからぶつかっていても、浮力なんか生まれるのか、と。
でも、30cm しか違わなくても、その軽い空気分子は、やはり、風船の下では、風船の上に比べて、たかだか軽い空気が 30 cm 分だけ「積もって」いるだけの違いでも、空気の動きには違いがある!下の方が、わずかと言っていいかもしれないけど、上に積もった空気に圧迫されることにより、空気の運動が「激しい」のです。下の方が動きが激しいから、物体は上に押されます。その上向きの力が浮力です。浮力は定量的には、風船の表面の圧力を、方向も含めて表面全部で合計したものです。すると、右からの圧力の全合計と、左からの圧力の全合計は、左右には物理的に違いがないので、反対方向の同じ力として相殺するから左右の方向、つまり横方向には物体を動かそうとする力は加わらないことになります。この時点で、右 \( + \) 左 \( = \) 0です。一方、上と下はというと、重力が下方向に働いていることから、上と下は物理的に同じとは言えません。上からの圧力と下からの圧力の表面での全合計は左右の時のように 0 ではありません。重力のために下の空気分子がより圧迫されているために、下の分子の動きは激しく、つまり下からの圧力の方が大きく、下からの圧力の合計の方が上のそれを上回っていまる。そして、圧力の合力をすべて合計すると、右 \(+\) 左 \(+\) 下 \(+\) 上 \( = 0 + \) 下\( + \) 上 \( = \) 上向きの力となり、それが浮力となります。
箱の中に砂を敷き詰める、砂の深さを、ある程度の深さにします。そこにピンポン玉を少し深く、ピンポン玉のてっぺんが砂から出ないくらいに、入れます。
箱を振るうと、ピンポン玉は砂から浮いてでてきますよね?砂のつぶつぶも、空気分子と同じなのです。ただ、砂粒は動いていないけれど、空気分子は、絶えず動いている。空気分子は衝突しても、常に完璧に弾性的に跳ね返るので、エネルギーを失わずに飛び続けています。
砂粒は、動いていないけれど、箱を振るうことにより、細かい運動をするので、(流体力学的にも)空気と同じようなものになります。
ピンポン玉が上に出てきてしまうのは、(箱を振るうことにより)砂の深いところの砂粒の方が、浅いところの砂粒よりも激しく動くから、ピンポン玉が下から押されて、上の方に浮いてきてしまう、ということがイメージできるでしょうか。砂が、積もっていると、下の方の砂は、上の砂に圧迫されて、それが振るわれて動くとき、ちりちりと細かくも激しい動きとなるのです。
同じように、風船も、下の方が激しく動いている空気の分子によって上の方に押されて、上昇していくわけです。
風船の中身が空気だとしたら、風船は上がっていかないのは、浮力と、空気の重さが等しいからです。というより、「空気中」のどんな「空気の部分」を取ってみても全体の空気に対して止まっているのは、浮力と、空気の重さがつりあっていることを意味しているのです。
浮力が、物体の上部と下部の圧力差から生まれる、というのは、具体的には以上のようなことを示しています。圧力とは分子の運動が激しさで(※)、圧力差から浮力が生まれるというのは、物体の下の方が上よりも、媒質の分子が激しくあたってくるから物体が上に押されて、浮く、ということなのです。
※厳密には、圧力が大きい=分子の運動が激しい。圧力=分子があたってきて跳ね返るときに受ける力。
それでは次に、
なぜ浮力が、物体が押しのけた分の媒質と同じ重さに等しいか。
さて、水がいっぱいに張られている中の、さらに、ある体積の部分の水を考えます。

ある体積の部分の水の形は完全な球形であるとします。
浮力の大きさについて考えるときは、力の分解、合力、ということを考えなくてはいけません。
水の中の、完全な球形の部分の水を考えます。要は、水中の中に、極めて薄くて重さの無視できるビニール袋があり中が水で満たされていると考えていいです。
水の中の水は、微視的には、水分子が盛んに運動し衝突を繰り返していますが、巨視的にはまったく動いていません。水の中の部分的な水は静かに止まっているし、水が勝手に動き出すはずもありませんね。対流もしていないことを考えます。
ビニール袋の重さが無視できるのだから、つまりは水は水の中に動かずに漂っていることがイメージできると思います。
さて、まったく動いていないとは、どういうことかというと、球形の部分の水に働く力が 0 ということなのですが、でも、これは「力が全く働いていない」ということを、必ずしも意味しません。球形の部分の水に働く力の、合計の力「合力」が 0 ということなのです。
では、球形の部分の水に働くちからにはどんなものがあるのか、考えなくてはいけません。力の分解です。\( 0 = F + (-F) \) と、方向が正反対の大きさが同じ力に分解する感じです。答えから言ってしまうと、働いている力は、重力と浮力の2つです。方向が正反対の力なのです。
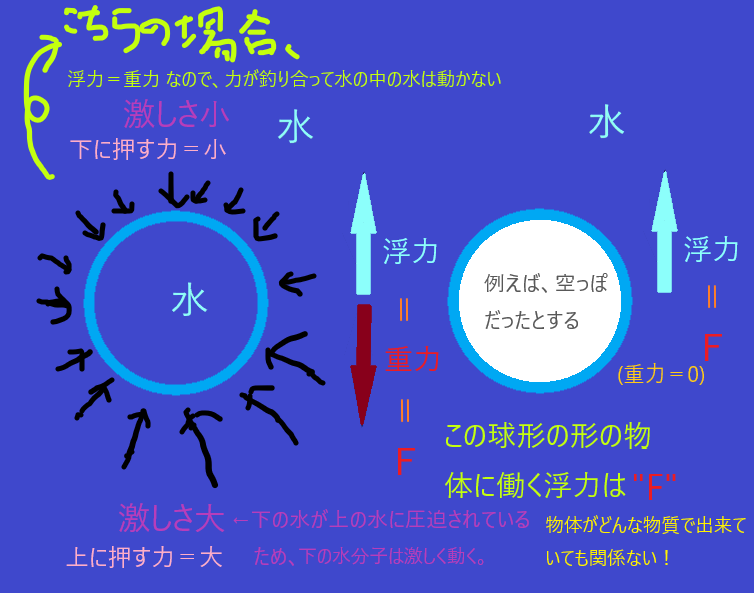
球形の部分の水には、地上の何物も逃れることができない、「重力」がまず、働いています。それでも、球形の部分の水が動かないのは、「重力」と同じだけの、上向きの力が働いていて、重力とキャンセルしているからです。その上向きの力こそ、「浮力」と言えるのです。つまり、水の中の球形の部分の水、にも、ちゃんと浮力は働いていて、それが、球形の部分に働く水の重さ \( =\) 重力と向きが逆で同じ大きさ (図中 \( F \) ) であり、したがって浮力と重力の合力が 0 であることから、球形の部分の水は動かないのです。高度な言葉を使うと、静水圧平衡の状態とも言います。
球形の水の部分に働く「重力」と、球形の水の部分に働く「浮力」が等しいということは、つまり、「浮力の大きさ」は球形の水の部分の水の重さに等しいということができます。
物体表面の単位面積当たりの、水からの圧力を全表面積にわたって合計するという計算をしなくても(浮力とはそもそもはそういうものですが)、それをしなくても、”ある形”に働く浮力というものが”ある形”の中の水の重さに等しい(水の中にある場合は)ということが、ここでわかりました。水の中の水が動かないという事実から、合力 \(= 0 \)、続いて、合力 \( = F \) (水にかかる重力) \( + \) \( (-F)\) (浮力) \(= 0 \) と考察することにより、浮力の “大きさ” (\( -F \) の絶対値 \( = |-F|\)) は袋の中の水にかかる重力つまり袋の中の水の重さと同じであることがわかったのです、合計の計算をしなくてもです。
油の中にあれば、油の重さに等しいことになります。つまり、溶媒でその”形”を満たした場合の重さです。
ここで、浮力というものはどういうものであったかを思い出してください。
物体上部と、下部の、空気や水分子の運動の激しさの差により生じる力でした。
ということは、物体がどんな物質でできていても、物体の形状が同じならば、その物体に働く「浮力」は同じ大きさなんだということが理解できます。
(また、どんな物体であれ、その表面で空気や水分子がその表面で弾性的に跳ね返される様子は変わらないと考えて大丈夫です)
水中の球形の部分に水が満たされていたときに、この部分に働く浮力は、その部分の中に満たされた水の重さそのものに等しかったわけですが、この部分が、かりにプラスチックで出来ていようが、鉄で出来ていようが、木で出来ていようが、かりに空っぽだったとしても、その部分に水が満たされた場合の重さが、浮力と等しいことはわかるでしょうか?形状が同じだから浮力が同じなのです。
ということで、媒質中の物体に働く浮力を知るには、その物体の形(の容器)に媒質(空気や水)を満たして、重力、つまり重さを測ればよいということになります。つまり、媒質中の物体に働く浮力は、その物体が押しのけた媒質の重さに等しい、そういうことが言えるのです!
以上で、浮力の説明を終わります!お読みいただきありがとうございました。


ディスカッション
コメント一覧
まだ、コメントがありません