【統計力学】デバイ模型により固体の比熱を求める
デバイ模型を使って固体の比熱を求めてみましょう。
デバイ模型とは何かというと…
固体の比熱を求める際の熱振動を考えるときのモデルとして、アインシュタイン模型というものがありますが、こちらは単純に各原子がすべて、温度により定まる一定の振動数で振動しているというものです。これに対してデバイ模型は、固体を、各原子がバネでつながれたような連続体のように考え、それらの、異なる振動数の振動が混ざっている、連成振動が熱を担っていると考えるモデルです。より難しく言えば、固体の熱振動を固体の中の音波で近似するとか、あるいはフォノンとして扱うなどという言い方をします。
アインシュタイン模型を用いて計算した、比熱の温度依存性はわりと実際のそれ(実験値)をよく表していますが、特に低温での比熱の挙動に関して、デバイ模型はより正確な結果を提供します。
それでは、デバイ模型を用いて「比熱」を計算してみましょう。
さきにも述べたように、固体の原子はバネでつながれたような形で連成振動をして温度を担っていると考えます。原子が振動してぶるぶるいうのが熱ですよね。さて、比熱は、温度 \(1 \) 度を上昇させるために必要なエネルギー、つまり \( dE/dT \) だから、まずはその全連成振動のエネルギー \( E \) を求めてみればいいでしょう。
ここからはいわゆるフォノンの扱いとなります。
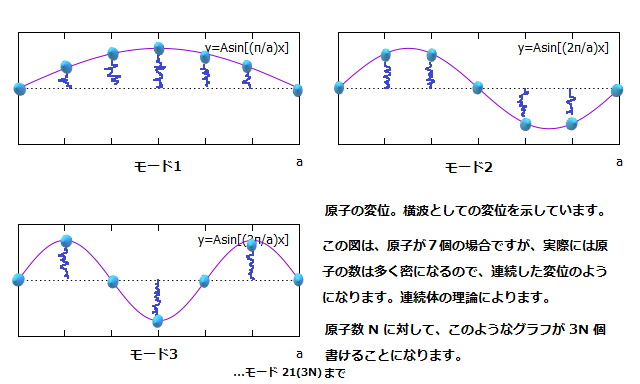
後でも述べますが、連成振動の問題はその振動を分解したものである、モード、つまり基本となる定常波、の重ね合わせの問題として扱うことができます。ギターの音を出す弦の振動が定常波の条件を満たす弦の振動の出す音である倍音の重ね合わせで成り立っているのと同様です。熱を担っている連成振動の「モード」とはつまり、固体の壁で、変位が \( 0 \) となるような定常波の形になっている振動です。以上のことの詳しい内容は連続体の理論に譲ります。以下の図がその、モードです。グラフには、\( x \) 軸の \( 0 \) が書いてありませんが、\( x = 0 \) である左端が左側の壁、右端である \( x=a \) が長さ \( a \) の部屋の右側の壁を示しています。ただし一次元の部屋です。
定常波になっているとはどういうことかといえば、変位を \( \phi \) 、振幅を \( A \) であるとしてモードの波を、
\[ \phi = A\ sink_xx\ sink_yy\ sink_zz\] として表したとき、固体の壁で変位が \( 0 \) である条件を求めればよく、これは、固体を一片の長さ \( a \) の立方体として
\begin{equation} k_x = \frac{n_x \pi}{a},\ k_y = \frac{n_y \pi}{a},\ k_x = \frac{n_z \pi}{a} \end{equation} という条件となります。( \( n_x, n_y, n_z \) は整数 )
\( n_x, n_y, n_z \) の組一つで、ある一つのモードが表されるということになります。
モード一つのエネルギーが〇〇で、そのモードが××個あるから、全連成振動のエネルギーは〇〇 × ×× \( = \) ◎◎、のような議論を展開したいので、ここで、モードの数について考えます。
なぜモードについて考えるのかというと、あとでも繰り返し述べますが、連続体の理論から、3次元の \( N \) 個の質点系の連成振動の問題は、\( 3N \) 個の独立な \( 1 \) 質点系の調和振動子、つまり \( 3N \) 個のモードの問題として扱えるからです。調和振動子の問題であれば、エネルギーを計算することができるのです。※ \( 3N \) 個の \( 3 \) は \( 3 \)次元であることから来ています。一次元の鎖状の質点系では、質点の個数 \( N \) に対して、モードの数も \( N \) となることは解析力学からよく知られていることです。
モードの数について考えるにあたり、まず、波の一般論として、波数とその成分の間の関係は、
\begin{equation} k^2 = k_x^2 + k_y^2 + k_z^2 \end{equation} です。
また、\( k \) について、これも一般論から波数と波長の関係として、
\begin{equation} k = \frac{2\pi}{\lambda} \end{equation} です。
固体内では縦波と横波で振動の伝わる速さが違いますが、これを \( v_0 \) として近似してしまいます。そしてまた、波の一般論から、波の速さ・角振動数・波長の関係として、
\begin{equation} \frac{\omega \lambda }{2\pi} = v_0 \end{equation} が言えます。
\( (3) \) 式と \( (4) \) 式から、\( k = \omega/v_0 \) が言え、これを \( (2) \) 式 に代入すると、
\[ \Bigl(\frac{\omega}{v_0}\Bigr)^2 = k_x^2 + k_y^2 + k_z^2 \] となります。\( (1) \) の内容をこれに代入すれば、
\begin{equation} \frac{a^2}{\pi^2} \Bigl(\frac{\omega}{v_0}\Bigr)^2 = n_x^2 + n_y^2 + n_z^2 \end{equation} が求まります。
\( n_x, n_y, n_z \) は、モード \( \phi = Asin\frac{n_x}{a}\pi \frac{n_y}{a}\pi \frac{n_z}{a}\pi \) の \( n_x, n_y, n_z \) のことですが、つまり、整数の組一つ \( (n_x, n_y, n_z ) \) は、一つのモードを表しています。
正負の同じ大きさの \( n_{xyz} \) は全く同じモードを表す数です。つまりモードを表す、ある \( n_{xyz} \) に対して \( n_{xyz} \) をとっても \( -n_{xyz} \) をとっても表されるモードは全く同一なので、重複して数えないために、
\[ n_x \ge 1,\ n_y \ge 1,\ n_z \ge 1 \] とします。この条件は、\( n_x,\ n_y,\ n_z \) のいずれかが \( 0 \) であると \( \phi \) は波にならないからカウントにいれないということも含んでいます。
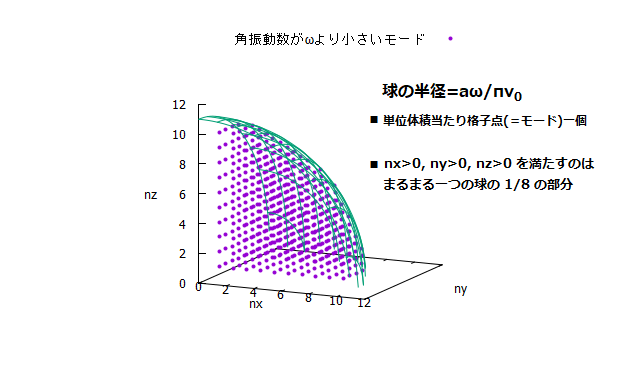
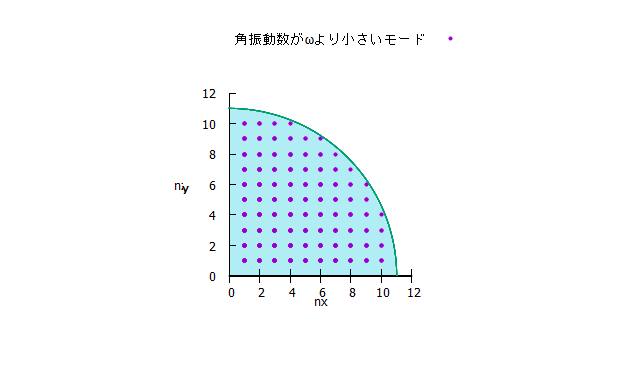
\( (5) \) 式は、モードを指定する \( n_x, n_y, n_z \) とモードの角振動数 \( \omega \) の関係ですが、この式が、点 \( n_x, n_y, n_z \) の原点からの距離 \( r \) が \( r = \frac{a}{\pi}\frac{\omega}{v_0} \) なのであるということを意味していることに注意すると、格子点の数、つまり「モードの数」というものについて以下のような図で考えることができます。両図とも、紫色の点１つ１つが一つのモードを示しています。
本来3次元のものを２次元にしてみたものが下の図ですが、下の図の水色の範囲(または上の図の球の内部の範囲)は、角振動数が \( \omega \) より小さいような範囲を表しており、この範囲にある格子点 \( (n_x, n_y, n_z ) \) は、\( \omega \) より小さい角振動数のモードを表していることになりますね。そして、その格子点つまり、モードの数は、体積 \( 1 \) につき格子点が \( 1 \) 個あることに気づけば、角振動数が \( \omega \)より小さいようなモードの数は、式 \( (5) \) より、半径 \( r = \frac{a \omega}{\pi v_0 } \) の球の体積の \( 1/8 \ [n_x \ge 0,\ n_y \ge 0,\ n_z \ge 0 の範囲] \) であると計算できます。
つまり、角振動数が \( \omega \) より小さいようなモードの数 \( G(\omega) \) は、
\begin{equation} G(\omega) = \frac{1}{6} \frac{a^3}{\pi^2} \Bigl( \frac{\omega}{v_0} \Bigr)^3 \end{equation} です。
これより、\( \omega \sim \omega + d\omega \) の範囲にあるモードの数は、\( (6) \) 式を微分して、
\begin{equation} dG = \frac{a^3}{2\pi^2} \frac{\omega^2}{v_0^3} d\omega \end{equation}
と計算できます。\( dG \) の表式の \( d\omega \) を除いた部分は 状態密度にあたりますが、\( (7) \) 式は、角振動数が \( \omega \sim \omega + d\omega \) の範囲に、モードが、
\begin{equation} \frac{a^3}{2\pi^2} \frac{\omega^2}{v_0^3} d\omega \end{equation} 個あるということを示しています。
さて、さきほども述べましたが、\( N \) 個の原子からなる固体の熱振動の連成振動の問題は、\( 3N \) 個のモード、つまり \( 3N \) 個の調和振動子の問題として扱うことができるので、角振動数 \( \omega \) の調和振動子のエネルギー \( \epsilon(\omega) \) についてわかれば、連成振動の全エネルギー、つまり\( N \)個の原子からなる固体の熱振動のエネルギー \( E(T) \)は、「モード一個のエネルギー \( \epsilon(\omega) \) \( \times \) 個数(\((8)\)式)」 を積分して求めればよいことになり、\( (8) \) 式を用いて、
\begin{equation} E(T) = \int \epsilon(\omega) \frac{a^3}{2\pi^2} \frac{\omega^2}{v_0^3} d\omega \end{equation} のように求めることができることになります。
角振動数 \( \omega \) の調和振動子のエネルギー(平均値) \( \epsilon(\omega) \) は、求め方は こちら で説明するとして、結果だけ示せば、
\begin{equation} \epsilon(\omega) = \frac{\hbar \omega}{2} + \frac{\hbar \omega}{e^{\beta \hbar \omega} – 1 } \end{equation}
です。
さて、当初の目標であった、固体の熱振動の全エネルギー \( E \)は、\( (9) \) 式のように求まりました。これを \( T \) で微分すれば、比熱を求めることができます。すなわち、
\begin{equation} C(T) = \frac{dE}{dT} = \int \frac{d\epsilon(\omega)}{dT} \frac{a^3}{2\pi^2} \frac{\omega^2}{v_0^3} d\omega \end{equation}
\( (10) \) 式の結果を微分すれば \( d\epsilon(\omega)/dT \) です。これは、調和振動子一個分の比熱に当たります。\( k_B \) はボルツマン定数です。これを計算すると、
\[ \frac{d\epsilon(\omega)}{dT} = k_B(\beta \hbar \omega)^2 \frac{e^{\beta \hbar \omega}}{(e^{\beta \hbar \omega}-1)^2} \]
最終的に、これを \( (11) \) 式に代入すれば、
\begin{equation} C(T) = \int k_B(\beta \hbar \omega)^2 \frac{e^{\beta \hbar \omega}}{(e^{\beta \hbar \omega}-1)^2} \frac{a^3}{2\pi^2} \frac{\omega^2}{v_0^3} d\omega \end{equation} となります。
ここで、式 \( (12) \) は \( \omega \) に関する積分ですが、積分範囲は書かないでおきました。しかし、モードの数が \( 3N \) であるという制約を用いると、\( \omega \) に制約が出て、\( \omega \) の最大値が存在することがわかります。すなわち、角振動数が \( \omega \) 以下であるモードの数が \( (6) \) 式の \( G \) で表されたのだから、
\[ G(\omega_D) = \frac{1}{6} \frac{a^3}{\pi^2} \Bigl( \frac{\omega_D}{v_0} \Bigr)^3 = 3N \] とおけば、\( \omega_D \) がそのような最大値となります。\( \omega_D\) をデバイ周波数と言います。角振動数 \( \omega \) が、\( 0 \sim \omega_D \) の範囲をとるならば、全モードは先ほどの図でその範囲内にある格子点で表されることになり、その数は \( G(\omega_D) = 3N \) となる、というわけです。
計算の結果、
\[ \omega_D = \frac{v_0}{a}(18 N \pi^2)^{\frac{1}{3}}\] となります。
※よくある論文や教科書等による解説では係数の数字は\(6\)となっておりここでは \(18\) となっていますが、これは、ここでは \( N \) を原子の数としているためです。数字が \(6\) となっているような解説では \( N \) はモードの数となっています。
この \( \omega_D \) を用いて 式 \( (12) \) の \( v_0 \) を消去することができて、計算の結果、式 \( (12) \) は、今求めた積分範囲も明示すれば、
\begin{equation} C(T) = \int_0^{\omega_D} \frac{9N}{\omega_D^3} \omega^2 \ k_B(\beta \hbar \omega)^2 \frac{e^{\beta \hbar \omega}}{(e^{\beta \hbar \omega}-1)^2} d\omega \end{equation} とすっきりとした形になります。
この計算のために、\( \beta \hbar \omega = x \) と置けば、\( (13) \) 式は、
\begin{equation} C(T) = \frac{9Nk_B}{\beta \hbar \omega_D } \int_0^{\beta \hbar \omega_D} x^4 \frac{e^x}{(e^x-1)^2} dx \end{equation}
これの積分の部分を、
\begin{equation} f(t) = \int_0^t x^4 \frac{e^x}{(e^x-1)^2} dx \end{equation} と表し( \(t = \beta \hbar \omega_D \) )、さらに、デバイ温度
\[ \Theta = \frac{\hbar \omega_D}{k_B} \] を導入すれば、
\begin{equation} C(T) = 9Nk_B \Bigl( \frac{T}{\Theta_D} \Bigr)^3 f\Bigl( \frac{\Theta_D}{T} \Bigr) \end{equation} となります。これがデバイ模型による固体の比熱の結果です。
\( (15) \) の \( f(t) \) は初等関数では表されませんが、\( t = \beta \hbar \omega_D \to \infty \) すなわち 温度 \( T \to 0 \) のとき
\[ f(\infty) = \frac{4\pi^4}{15} \] という定数となります。これより、低温つまり、\( T \to 0 \) のとき、
\[ C(T) = \frac{12\pi^4}{5} k_B \Bigl( \frac{T}{\Theta_D} \Bigr)^3 \propto T^3 \] となり、比熱は温度の３乗に比例します。これは低温での固体の比熱のふるまいを非常によく表しており、デバイ模型の成功を示しています。
固体の比熱に関しては、19世紀のデューロン・プティの法則というものが知られており、これによると、固体元素の比熱(定積モル比熱)はどれもだいたい \( 3R\) (\(R\)は気体定数) であるというのですが、これは低温での固体の比熱の温度依存性を説明できず、これが古典論の限界でした。
そして、今回説明したように、量子力学により連成振動(格子振動)を量子化し、さらにデバイの理論が固体を連続体のように考えフォノンを導入したことによって、固体の比熱の理論は成功を収めることとなりました。
以上です。
