【量子論】レイリー・ジーンズの式~プランクの放射公式・黒体放射
量子力学の本にも、大学院の入試問題の解説にも説明があることはあるのですが、納得のいく説明に出会ったことがありません。わかる人はすごいなぁ、何か次元が違うんだ、のような感覚がある人もいるかもしれませんが、今言わせてもらえば、あんな不十分なもので分かったつもりになってる人は、物理学に対する姿勢がなにかおかしくはないでしょうか。
やることは箱の中の、光子のとれる道のようなものである”モード”にある光子の数を数えて、モードの数を、箱の中で形成可能な定常波の数として調べてから光子の数にそのモードの数をかけて全エネルギーを求めるという、普通にその意図がわかることをやっているのですが、いろいろ掘り下げなければならないところがあるからその意図をいつも押さえておかないとぶれてわからなくなっていく。
ここでは、プランクの放射公式とはそもそも何を知りたくて考えだしたのかというところから、心ある人間として導出していきたいと思います。この記事は黒体放射の超かみ砕いた超親切な導出です。
プランクの放射公式は、鉄鋼業の盛んになってきた19世紀、鉄工所の熱い炉の温度を正確に知る必要があるという状況下で、溶鉱炉内の”色”(つまりあのだいだい色)から”温度”を知るための、色と温度の関係に関する研究から生まれたものです。
だからここでは、炉の色から炉の内部の温度を知るにはどうするかという状況設定からすすめていきます。
炉があって、ある温度で、そこから光が出て色をもっている。光のスペクトルは観測できるから、その観測から内部の温度を知りたい。
色とはつまりはスペクトルのことになりますね。そして、炉から出てきた光のスペクトルは観測できる。スペクトルとは結局なにかというと、波長を分割して、波長ごとに、ある時間内に検出されるその波長の光子の粒の数を集計してエネルギーを合計したものをグラフにしたもので、つまり波長別の光のエネルギー強度の分布なのです。したがって、温度を含む形でそのスペクトルの式、すなわち、穴から出てくる光の、ある波長の光のエネルギー強度(単位時間に出てくるその波長の光のエネルギーの合計)がどれだけになるのかが求められればよい、という状況です。そしてそれは、温度 \( T \) に依存している。具体的には、穴から出てくる電磁波の、波長が \( \lambda \) であるもの、のエネルギー強度が ( \( T \) を含む形の)どのような式で表されるかを導きたい。それができれば、エネルギー強度の観測値と理論値を比較して、逆に 温度 \( T \) を定めることができる。【大問題】
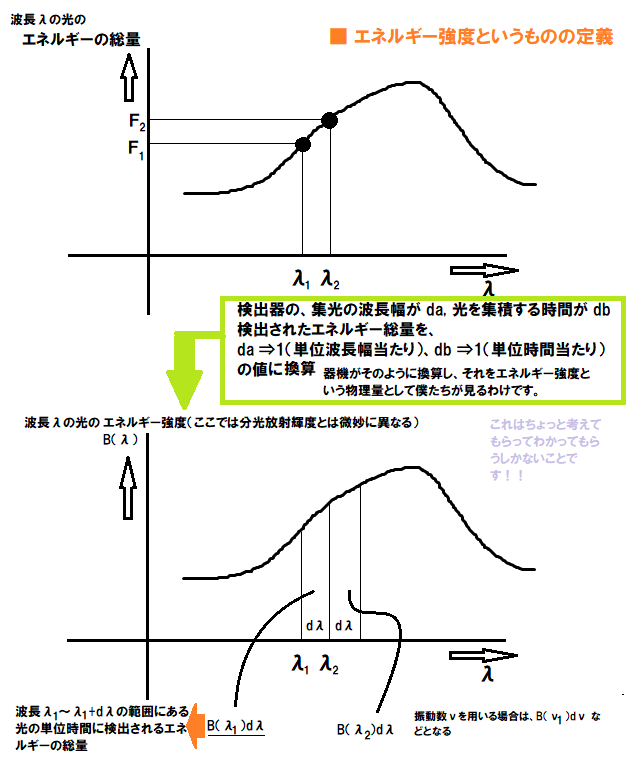
(上図のB(λ)は、本来の分光放射輝度B(λ)に検出器の集光部分(カメラ)が光源(穴)に対して見込む立体角をかけたものです)
炉をモデル化し、ある大きさの鉄の箱があり、内部はある温度になっていて、小さな穴が開いていて、そこから光が出ている、という空洞放射のモデルにします。なぜなのか、と、少し飛躍に見えるかもしれませんが、これは19世紀の研究の結果であって、そこを見習っています。いやもちろん、炉の、穴以外の部分も同じようにだいだい色に光っているでしょうが、ここでは穴から出てくる光を考える(のでしょう、教えてくれる先生がいない)。
プランクの放射公式は、この空洞放射の考察から導かれます。空洞放射とは、箱(鉄の箱でいい)の内部がある温度で、小さな穴が開いているときに、その穴から出てくる光(熱輻射)のことです。
空洞放射の測定では、温度 \( T \) の熱平衡状態にある空洞内の輻射が、空洞に開いた小さな穴から外に出てきたものを観測するのですが、穴からのぞいたら、穴の向かい側の壁からの放射が見えるだけのような気がします。しかしそれでよいのです。向かいの壁から見えるのは温度 \( T \) の壁からの放射そのものです。周りを取り囲まれて、壁が、温度 \( T \)の黒体放射をしているのです。空洞内では、空洞内部表面からの熱輻射(電磁波)と空洞をから壁に吸収される電磁波の間で平衡状態が成り立っていると考えることができます。壁から出る波と壁に入る波が、方向だけ正反対なだけの、同じ波であると考えることにより、方向だけ逆の他は同じ波を重ね合わせると定常波になることから、空洞内を満たす電磁波が定常波になっていると考えることができます。そして「空洞に充満する電磁波(この定常波)」を解析することにより、温度 \(T \) の壁からの(黒体)放射の性質がわかることになるのです。そうして導かれたのがプランクの放射公式です。 穴から出る光と温度の関係について調べるといってはてどうしたものか、という最初の問題から一歩進み、空洞に充満する電磁波について考察してみたらわかるかもしれない、という可能性に変わりました。以下、実際これを試みると、結果を導くことができます。
熱を輻射する物体のモデルとして、すべての波長の電磁波を完全に吸収する黒体という概念が用いられます。空洞輻射のちいさな穴も、入った光は出てこれず完全に中に吸収され(穴が小さいので出てこれないということでいい)、黒体とみなされます。空洞放射と黒体放射とはほぼ同義で使われます。
理論的に正しいプランクの式を導く前に、実は、観測事実を正しく説明できなかったレイリージーンズの式をまず導きます。レイリージーンズの式では、どのモードも同じエネルギーを持っていると仮定した点が間違いのもとでした。ただ、その点を修正すると、正しい答えが導かれるのです。その間違いの点までの理論は、正しかったのです。
それでは、空洞を満たす光について考察していきましょう。
空洞は、一辺が長さ \( a \) の立方体の容器であるとします。
まず、空洞内の波長 \( \lambda \) の光について考えることにしましょう。空洞内の電磁波は定常波になっていると考えるので、波長 \( \lambda \) の “定常波”について考えます。定常波だけを考えればいいのはどういうことかというと、例えば、笛から出てくる音階も、増幅されない雑多な波は無視して、増幅されて卓越する定常波を考えればよい、と同類のことと考えることができます。
波長 \( \lambda \) の光(光子)のすべてエネルギーの合計(これはイメージするなら波長 \( \lambda \) の光子の一つのエネルギーは \( hc/\lambda \)で一定だから、それのその光子の数の分だけです。つまり光子の個数をかけたもの)がスペクトル中での 波長 \( \lambda \) における光の強度にほかなりません。それを知るには、空洞内で形成可能な定常波の数を調べ、一つの定常波がどのようなエネルギーを持っているか調べれば、定常波の数×定常波一つ分のエネルギー として波長\( \lambda \)の電磁波のエネルギーの合計を求めることができるはずです。まずはここでは \( \lambda \) が違っていてもすべてのモードはそれぞれ同じエネルギーをもっているとします(これは量子論的には誤りであることを後で述べます)。
※ 波長 \( \lambda \) の光の全エネルギーを求めるというのはほんとうはできませんので、つまりこれより後で行っていることは、波長 \( \lambda \) と \( \lambda + d\lambda \) の間にある光のエネルギーを合計するということです。
当時の古典統計力学の「エネルギー等分配則」によると、平衡状態の力学的な振動子一個当たりには、 “平均” \( k_BT \) のエネルギーが分配されるということでした。そこで、レイリーは平衡状態では電磁波は、容器の端で変位が0となるような定常波として存在するとした上で、定常波を調和振動子と考え、空洞内では定常波同士が調和振動子として相互作用しながら定常状態を作っているとして、一つの定常波につき \( k_BT \) のエネルギーが等分配されるとしました(のだろう)。
レイリーの考え方を整理すると、平衡状態では空洞は定常波で満たされ、定常波であるような電磁波が、一つ一つが \( k_BT \) のエネルギーを持っていることになるから、(波長 λ の電磁波の)全エネルギーを知るには、定常波の個数を調べ(モードを数える)、その個数に \( k_BT \) をかければよいことになります。
ではまず定常波の個数を調べます。
定常波の個数すなわちモードを数えることは、適切に考えていくと、\( x, y, z \) 座標3次元空間の、立体的な図の格子点の数を数えることに帰着します。
まず、空洞の中の3次元の定常波が、時間に依存する部分を除いてどのように書かれるかを明確にしておきます。空洞は、一辺が長さ \( a \) の立方体の容器でした。
そうすると、定常波の変位は以下のように書かれるでしょう。平面波とします。ここでは \( u \) は電場または磁場の変位のことですが、変位の大きさはこの問題では終始問題になりません。
\[ u = Asin(k_xx)sin(k_yy)sin(k_zz) \]
\( k_x \), \( k_y \), \( k_z \) は波数です。定常波であるということは、一辺が \( a \) の長さの立方体の端で変位が 0 、つまり波の節となるということなので、\( n_x \), \(n_y\), \(n_z\) を整数として、\( k_xa = n_x\pi \), \(k_ya = n_y\pi\), \(k_za = n_z\pi \) を満たします。満たさなくてはいけません。そういう条件を満たす波である定常波を数えるにはどうしたいいでしょうか。
\( n_x \), \( n_y \), \( n_z \) が負であっても \( n_x \), \( n_y \), \( n_z \) が正である場合とまったく同じ条件を意味しますから、\(n_x\), \(n_y\), \(n_z\) は正の整数であるとします。そうしないと、節の条件を満たす \( k_x \), \( k_y \), \( k_z \) を数えるときに、同じ定常波を意味する正と負の 二つの \( k_… \) を数えてしまいます。
波長を \( \lambda \) で固定しておいての、この節の条件を満たす \( k_x \), \( k_y \), \( k_z \) の組はいろいろありますが、その \( k_x \), \( k_y \), \( k_z \) の組を全部数えるのが、定常波(モード)の数を数えるということになります。異なるそれぞれの定常波というのは、\( k_x \), \( k_y \), \( k_z \) のそれぞれ異なる定常波ということだからです。
それぞれの、\( n_x = 1, 2, 3,… n_y = 1, 2, 3,… n_z = … \) に対して \( k_x, k_y, k_z \) が一個ずつ定まることになりますが、\( k_x, k_y, k_z \) は勝手にとって良いものではなく、波数なので波長 \( \lambda \) に縛られています。
だからまず、\( \lambda \) と \( k_x\), \( k_y \), \( k_z \) の関係を調べます。
この定常波は波なので、波動方程式を満たします。某問題集の解説でシュレディンガー方程式を持ち出しているものがあったが、まったくデタラメである!
\[ \frac{d^2u}{dt^2} = c^2 ( \frac{d^2u}{dx^2} + \frac{d^2u}{dy^2} + \frac{d^2u}{dz^2}) \]
この波動方程式に 定常波の式を代入します。ところが、そのためには、定常波の式に時間依存の部分 \( asin\omega t+bcos\omega t \) を加えたもの、\( (asin\omega t+bcos\omega t)sin(k_xx)sin(k_yy)sin(k_zz) \) を考えなければならず、これはここに書くにはエレガントでないので ここ に書くことにし、結果だけ参照します。これは波動に関する一般的知識です。
結果として、
\begin{equation} k_x^2+k_y^2+k_z^2 = k^2 = (\frac{2\pi}{λ} )^2 \end{equation}
であることがわかります。これを満たす \( k_x, k_y, k_z \) を数えたいのですが、この式ではちょっと数えられません。
\( k_xa = n_x\pi \), \(k_ya = n_y\pi \), \(k_za = n_z\pi \) だったから、\( k_x = n_x\pi/a\), \(k_y = n_y\pi/a \), \(k_z = n_z\pi/a \) です。これを \( (2) \)に代入すれば、
\[ (n_x^2 + n_y^2 + n_z^2) = ( \frac{2a}{λ} )^2 \] となります。\( n_x \), \( n_y \), \( n_z \) は正の整数です。定常波の条件を満たす \( k_x \), \( k_y \), \( k_z \) の組を数えることは、この、整数である \( n_x \), \( n_y \), \( n_z \) の組の数を数えることを意味します。
少しややこしいかもしれませんが、この式は、半径 \( 2a/\lambda \) の球の中の、\( n_x>0 \), \( n_y>0 \), \( n_z>0 \) の数、つまり第一象限内のすべての格子点の数が、波長 \( \lambda \) 以上のすべてのモードの数となることを表しています。第一象限が全象限の \( 1/8 \) にあたることに留意して、
(実際は3次元球を考えますが、3次元の図を描くとぐちゃぐちゃで説明できませんので、\( n_z = 0 \) の平面上の部分の2次元の図を描いています。追記:あと、\( n_z \gt 0 \) であるし、格子点は \( n_x \) と \( n_y \) が 0 のものを含んでいますが、\( n_x \gt 0,\ n_y \gt 0,\ n_z \gt 0 \) なので厳密には違います。格子点一つが一つのモードを表し、単位体積あたりに一つの格子点つまりモードがあるというイメージをとらえてください。)
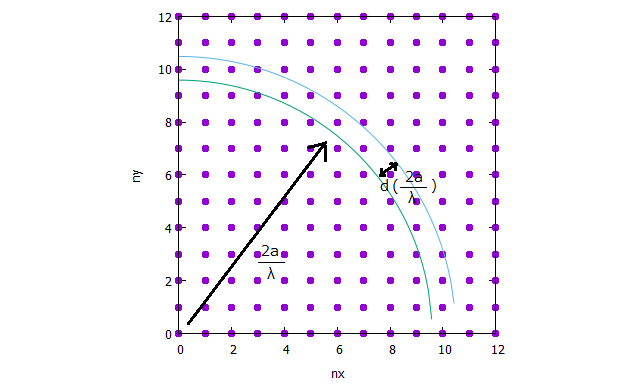
その数は、
\[ N = \frac{1}{8} \frac{4}{3} \pi (\frac{2a}{λ})^3 = \frac{1}{8} \frac{4}{3} \pi ( \frac{2a\nu}{c} )^3 = \frac{4}{3} \frac{\pi a^3\nu^3}{c^3} \]
求めたいものは 波長 \( \lambda \)(振動数 \(\nu\) ) のモードの数なので、\( \nu \) の幅 \( d\nu \) を考慮、すなわち範囲 \( d\nu \) に含まれるモードの数を勘定すればいいから、\( N \) を微分して、\( dN = 4\pi a^3\nu^2d\nu/c^3 \) となります。1つの電磁波のモードは、2つの偏波(偏光)を持つので、これを2倍します。つまり、今数えた1つの電磁波のモードには、偏光の独立な2つの光子が入れることを意味します。
\[ 2 \times 4\pi a^3\nu^2d\nu/c^3 = 8\pi a^3\nu^2d\nu/c^3 \]
これが、波長 \( \lambda \) の ( \(\lambda\sim\lambda+d\lambda\)、または \( \nu\sim\nu+d\nu\) 間にある) 定常波(モード)の数です。
これに、1つのモードの平均エネルギー \( k_BT \) をかければ、炉から出る波長 \( \lambda \) の光の強さ
\[Id\nu = \frac{8\pi \nu^2a^3}{c^3} k_BT d\nu \] となります。\( a^3 \) は空洞の体積で、これは空洞の体積が大きければそれに比例してエネルギーが増えることを意味しているに過ぎないからスペクトルの”形”には寄与しません。よって、一般的には \( a^3 \) で割った、\[Id\nu = \frac{8\pi \nu^2}{c^3} k_BT d\nu \] を結果として用います。
しかし、この結果は、レイリー・ジーンズの法則といい、波長が長いところでは観測結果とよく一致しますが、波長が短い時に実験結果と合いません。
このため、エネルギー等分配則を用いるのが改められました。プランクは、振動数 \( \nu \) を持つ調和振動子のエネルギーは \( h\nu \) を単位としてやり取りされるという量子仮説を導入しました。アインシュタインが光子の存在を仮定する5年前のことです。
さて、量子力学の「量子」とはどんな意味なのか。それは、上記に述べた仮説にあるように、やりとりされるエネルギーに単位があることが答えです。つまり、「量子」とはエネルギーという “量” の単位「子」という意味なのです。この仮説が導入されたのが光子の仮説よりも前で、エネルギーを運ぶ電磁波の粒子性(光子)が明らかでなかった時にプランクにより試行錯誤で導かれた仮説です。そして、この1900年の子の仮説こそが、量子力学における初めての量子論的概念なのです。
光子のことを知っている我々にとって、光子のエネルギーが \( h\nu \) であることは少し混乱のもとかもしれません。光子一個のエネルギーが \( h\nu \) なら、エネルギーを分配することもなく電磁波の定常波のエネルギーはただ単に \( h\nu \) のままじゃね?と。
やりたいことは、波長 \( \lambda \) の定常波の、全エネルギーを求めるということです。
レイリーのエネルギー等分配の考えをやめ、次にやることはプランクの量子仮説を使って(波長 \( \lambda \) の)光のエネルギーの合計を考えることですが、定常波(モード)の考え方は引き継がれます。エネルギー等分配の時とは違い、こんどはある定常波のエネルギーは一定の \( k_B T \) ではなく、\( \lambda \) に依存する量となります。当時はこう量子仮説はまだでしたが、光が粒子であることを既知としたとして説明すると、これからこの一つのモードに光子がいくつ入るのか、ということをやります。光子が分配されるのです。直接光子の数自体を計算するのではなく、やはりどれだけのエネルギーが分配されるのかを計算することになるのですが、その計算の実質的な意味は、光子が一つの定常波(モード)にいくつ入るのか、ということになっています。一つの光子のエネルギーは確かに \( h\nu \) ですが、定常波は一つの光子で成り立っているのでなく複数の光子が担うので、電磁波のエネルギーがただ単に \( h\nu \) であるということではないのです。
ここで、今まで出てきた \( \nu \) は、波長 \( \lambda \) に対応する \( \nu \) であり、これ以降においても \( \nu \) = \( c / \lambda \) であることを断っておきます。
光子が出てきて、波の扱いとの両立で混乱するかもしれないので、豆知識として書いておきます。定常波はもちろん電磁波ですが、光子が担うと書きました。波=光子ですが、では光子が増えたり減ったりすると、それは波としてはどのように変化することに当たるのでしょう。答えは、振幅が増減します。電磁波において、光子の数は振幅(の二乗)に対応(比例)します。光子の粒子描像においては \( nh\nu \) がエネルギーを表し、波動の描像では振幅の二乗(に係数をかけたもの:\( \epsilon E^2 \) または \( \mu H^2 \)) がエネルギーを表すことからも、対応関係がわかるでしょう。
電磁波は壁に当たるたび、そこで壁にエネルギーを与えたり、壁から再び放出される際には壁からエネルギーを得たりしますが、プランクは、その与えたり得たりするエネルギーが、どんな値でもよいものではなく、\( h\nu \) の単位で行われる、つまり \( h\nu \) の整数倍のエネルギーがやりとりされる、と仮定しました。この「量子仮説」は先の一行で述べたとおりです。そしてこの仮定は、当時はまだわかっていませんでしたが、これはつまりは、電磁波の正体が光子という粒子(のあつまり)で、一つの光子のエネルギーが \( h\nu \) であったということそのものなのです。
さて、エネルギーのやりとりが \( h\nu \) の単位で行われるとした場合、なにがどうなるのでしょうか?エネルギーが \( h\nu \) の単位でやりとりされるならば、各定常波のエネルギーは、\( h\nu \), \( 2h\nu \), \( 3h\nu \) … というとびとびのエネルギー値しかとりえないということになります。炉の壁の鉄の分子がうごめき光子が飛び交っていて、一つの定常波は、瞬間瞬間変わりながら、\( h\nu \), \( 2h\nu \), \( 3h\nu \)… といった大きさのエネルギーの光を出しています。それが、観測する光です。ただし、\( h\nu \) から \( 何h\nu \) に飛んだりする様子はもちろん観測機器には表れません。観測される値はじっと動かないようにみえてますが、それらは細かく変動していて、観測されるのは移り変わるエネルギー値の”平均”の値なのです。炉内に充満する定常波には波長 \( \lambda \) が同じでも異なるモードの定常波がありますが、モードは異なってもエネルギーは \( \lambda (\nu) \) だけに依ることが後の計算でわかります。だから、一つの定常波の平均エネルギーを求め、定常波の数をかければ、ずーっと求めたいと思ってきた波長 \( \lambda \) の定常波の、全エネルギーを求めることができる(それがスペクトル)。定常波の”数”は、さっき計算したやつ(\( 8\pi\nu^2/c^3 \times d\nu \))でいいです。エネルギーは、さっきは \( k_BT \) ですべてのモードで等しいとしていましたが、今回のように考える場合、\( k_BT \) のように一定である保証はありません。実際に平均値を計算しなくてはわかりません。さきに、誤っていたところを量子論的に正しく考える時が来ました。
定常波が、温度 \( T \) の壁と熱の授受を行いながら熱平衡状態にあり、その定常波のエネルギーが、\( h\nu \), \( 2h\nu \), \( 3h\nu \)… といったとびとびの値をとるという状況である場合、こういうものを扱うのは統計力学です。
定常波のエネルギーもじっと一定ではなく変化しますが、やはり温度 \( T \) という条件がありますから、定常波にとって一番落ち着きやすいエネルギーの状態、つまり平均エネルギーがあります。そして、その平均エネルギーを、統計力学の方法で求めようというのです。そしてその平均エネルギーを以って電磁波の定常波一個のエネルギーとします。
定常波一個のエネルギー平均値を求めるには、(統計力学の)等重率の原理からミクロカノニカル分布を経て導かれる、カノニカルアンサンブルの方法を用います。カノニカルアンサンブルの方法では、 \( E_i \) が離散的なとびとびエネルギー状態であるとして、温度 \( T \) の熱浴に接している系がエネルギー \( E_i \) をとる確率は、\[ P(E_i) = \frac{exp[-\frac{E_i}{k_BT}]}{\sum_i exp[-\frac{E_i}{k_BT}]} \] としてこれを求めることができるのです。確率がわかれば、エネルギーの平均値が求められることになります。すなわち、\( <E> = \sum E_nP(E_n) \) です。
\( E_i \) は各量子状態のエネルギーで、今回の問題では \( E_1=h\nu, E_2=2h\nu, E_3=3h\nu … \) です。この式のエッセンスは… 式を見ればわかりますが、\( E_i \) によって変わってくるのは、分子だけです。分母は和だからです。式は等式ですが、分母を取り払って理解するなら、\( P(E_i) \propto exp[-\frac{E_i}{k_BT}] \) 。\( P(E_i) \) は、\( exp[-\frac{E_i}{k_BT}] \) に比例するということです。あるいはこれは相対確率です。ざっくり言ってしまうと、状態のエネルギー \( E_i \) が大きいほど、そのような状態は状態数がすくなく(エントロピーが高い)、得難いために、\( E_i \) が大きいほどその状態をとる確率が少なくなるということです。
カノニカルアンサンブルの方法は、大きい熱浴に接している系の、状態のとりうる数から確率を求めるということを行い、エントロピーとボルツマンの原理を交えて計算して導かれた方法です。
ごたくが多くなりましたが、あとは \( <E> = \sum E_nP(E_n) \) を計算するだけです。ただし、和の計算が技巧的になっています。
単位 \( h\nu \) でとびとびエネルギー状態をいったりきたりしている一つの定常波がエネルギー \( E_n = nh\nu \) をとる確率は、 \begin{equation} P(E_n) = P(\color{blue}{nh\nu} ) = \frac{exp[-\frac{\color{blue}{nh\nu}}{k_BT}]}{\sum_n exp[-\frac{\color{blue}{nh\nu}}{k_BT}]} \end{equation}
だから、\( E_n \) の期待値(平均値)は、
\[ <E_n> = \sum_n E_nP(E_n) \] \begin{equation} = \sum_n \frac{nh\nu exp[-\frac{\color{blue}{nh\nu}}{k_BT}]}{\sum_n exp[-\frac{\color{blue}{nh\nu}}{k_BT}]} = \frac{ \sum_n nh\nu exp[-\frac{\color{blue}{nh\nu}}{k_BT}]}{\sum_n exp[-\frac{\color{blue}{nh\nu}}{k_BT}]} \end{equation}
となります。この\( (3) \)式の分子の計算が技巧的になります。まず、\( \frac{h\nu}{k_BT} = x \) とおきます。\[ \sum_n nh\nu exp[-\frac{nh\nu}{k_BT}] = \sum_n nh\nu exp[-nx] = h\nu \sum_n n e^{-nx} \] そして、次のように変形していき、微分と和の順序を入れ替えてしまうことにより巧妙に計算できるようになります。
\( e^{-x} = r \) とすると、\[ h\nu \sum_n n e^{-nx} = \] \[h\nu \sum_n n r^n = h\nu r \sum_n n r^{(n-1)} = h\nu r \sum_n \frac{dr^n}{dr} = h\nu r \frac{d}{dr}(\sum_n r^n) \]
最後の式の和では、\( x \) が正の数であることから、\( r = e^{-x}\) は 1 より小さい数ということになるので、この和は収束します。\( n \) は 0 からです。カノニカルアンサンブルの方法が、\( n \) を 0 からカウントするからです。すると、和の値は等比級数の和なので \[ \frac{1}{1-r} \] と計算できます。よって、\[ h\nu r \frac{d}{dr}(\sum_n r^n) = h\nu r \frac{d}{dr}(\frac{1}{1-r}) = h\nu \frac{r}{(1-r)^2} \] ここまで、\( (2) \) 式の分子を計算しました。
一方、\( (2) \) 式の分母は \( \sum_n r^n \) であることがわかります。ゆえに、\[ (2) 式の分母 = \frac{1}{1-r} \]
以上のことから、\( (2) \) 式は、\[ h\nu \frac{r}{(1-r)^2} / \frac{1}{1-r} = \frac{h\nu r}{1-r} \] となります。\( r = e^{-x} = e^{-\frac{h\nu}{k_BT} }\) であったから、この値は \[ \frac{h\nu e^{-\frac{h\nu}{k_BT}}}{1-e^{-\frac{h\nu}{k_BT}}} = \frac{h\nu}{e^{\frac{h\nu}{k_BT}} -1 } \] となります。これが 波長 λ の定常波の1つの平均エネルギーであり、これに定常波の個数 \( \frac{8\pi \nu^2}{c^3} d\nu \) をかければ、波長 \( \lambda \) の定常波すべての合計エネルギー \[ I(\nu) d\nu = \frac{8\pi \nu^2}{c^3} \frac{h\nu}{e^{\frac{h\nu}{k_bT}} -1 } d\nu \] となり、こうして、黒体放射の式=プランクの放射公式を導くことができました!!
※ エネルギー \( E_n = nh\nu \) の状態とは、つまりは定常状態(モード)に光子が \( n \) 個分配されている状態です。
ここでは確率から計算しましたが、分配関数の公式を用いる方法もあります。やっていることは一緒です。
さて、波長 λ (振動数\(\nu \))の定常波の1つの平均エネルギーは、\[ \frac{h\nu}{e^{\frac{h\nu}{k_BT}} -1 } \] とわかりましたが、\( \lambda \) を無限大、つまり、\( \nu \) を無限に小さくした場合はどうなるでしょうか。
この場合、\( x \) が小さいとき \( e^x \sim 1+x \) となることを利用すれば、分母 = \( 1+ \frac{h\nu}{k_BT} – 1 = \frac{h\nu}{k_BT} \) となり、平均エネルギーは、\[ h\nu \times \frac{k_BT}{h\nu } = k_BT \] となります。
これは、エネルギーをやりとりする単位である \( h\nu \) が無限に小さくなると、エネルギーの授受がもはやとびとびでなく連続的に行われるとみなされるため、量子的効果がなくなり、定常波の平均エネルギーが古典的な結果である \( k_BT \) に一致するということを示しているのです。
しかし…まだ続きがあります。
プランクの式は、空洞内のエネルギー密度がどれだけなのかを示した式です。穴からの放射のスペクトルの”形”は説明はできますが、実際に穴から出てくる放射のエネルギー強度とは、比例定数の違いがあります。まだ穴からどれだけのエネルギーが出てくるかの値そのもの、検出器で測定される値、を計算できていないのです。穴の面積が \( dA \) であるとして、放射は \( dA \) にもちろん比例するだろうし、その部分の計算はまだです。
これから、穴の面積を \( dA \) として、方向 \( d\Omega \) に単位時間当たりに放射されるエネルギーを計算したいと思います。
プランクの式における空洞内のエネルギー密度は、全方向に放射される光子を含んでいます。だから、方向 \( d\Omega \) に放射されるエネルギーとしては、プランクの結果に \( \Omega/4\pi \) をかければ求まります。しかしまだです。この \( d\Omega/4\pi \) を掛けた値
\[ \frac{2 \nu^2}{c^3} \frac{h\nu}{e^{\frac{h\nu}{k_BT}} -1 } d\nu d\Omega \]
は、あるとき空洞内につまっていたエネルギーを解放しただけのもので、一度箱からエネルギーを解放した(箱を開けた)結果、箱の中が”から”になるようなものです。つまり、壁からは絶えず放射が行われているという要素を考えていません。
これを考えるには、光子が単位時間に進む距離(光速)が \( c \) であることを考え、面積が \( dA \) で、穴の反対側に伸びる 長さ \( c \) の円筒の中の光子が穴に届く様子を考えればいいのです。この円筒の中にある全光子が、単位時間に穴から出てくる全光子です。箱の中に充満する光子の、方向 \( d\Omega \) に放出されるようなものの、単位体積当たりのエネルギー密度は
\[ \frac{2 \nu^2}{c^3} \frac{h\nu}{e^{\frac{h\nu}{k_BT}} -1 } d\nu d\Omega (直前の式と同じ) \]
だったから、その値に体積 \( cdA \) をかければ面積\( dA \) の穴から \( d\Omega \) の方向に単位時間あたりに放射される光子のエネルギーが求まります。実は、この 円筒の説明はすこし単純化してずるをしています。体積 \( cdA \) の中に含まれる光子で、方向が \( d\Omega \) の方向に光子が飛んでいくっていうと、光子は直進するから、角度が大きい方向への放射は円筒の割と穴に近いところになければならないし…え?ってなります。輻射の考え方のことなので、多少考えなくてはなりませんが、複数の円筒などを考えて考えを整理していくと、結局 \( cdA\) にエネルギー密度をかける計算で大丈夫であることがわかります。
結果は、
\[ \frac{2 \nu^2}{c^3} \frac{h\nu}{e^{\frac{h\nu}{k_BT}} -1 } d\nu d\Omega \times cdA = \frac{2 \nu^2}{c^2} \frac{h\nu}{e^{\frac{h\nu}{k_BT}} -1 } d\nu d\Omega dA \]
これを \( d\nu d\Omega dA \) で割ると、
\[ B(\nu, T) = \frac{2 \nu^2}{c^2} \frac{h\nu}{e^{\frac{h\nu}{k_BT}} -1 } \]
これが、温度 T の黒体の表面の単位面積から単位時間に単位立体角に放射される単位周波数当たりのエネルギーで、 黒体放射の分光放射輝度といいます。炉からの光の観測はすなわち分光測定となりますが、観測されるエネルギー強度の理論値が、この式で与えられます。
おまけとして、この \( B(\nu, T) \) を \( \nu \) について積分し、全立体角の半分で積分する(つまり \( 2\pi \)をかける)と、温度Tの黒体の表面から放出される全エネルギーに関する、シュテファン=ボルツマンの法則
\[ K = \sigma T^4 \]
を導くことができます。
黒体放射の解説は以上となりますっっ!!!
壁の放射が黒体放射であるというのがわからない=>
温度Tの壁は、取り囲まれなければただの温度Tの、材質等にも左右されるような熱放射をしますが、周りを取り囲まれたことによって、材料によらず温度Tの黒体放射をするようになります。穴から見ているのは、壁でありその黒体放射です。同じ温度 \( T \) でも取り囲まれるか取り囲まれないかで放射は変わるということです。ただし、一度黒体放射の式を導出してしまえば、黒体放射でないただの熱放射でもそれに近いとみなし、近似として黒体放射の式で熱放射を計算してしまいます。


ディスカッション
コメント一覧
プランクの式が実験事実を正確に表現しているとして、古典的な式であるレイリー・ジーンズの式とウィーンの式が適用できる範囲を考察せよ。例えば、温度 T 5000K で、1%以内の誤差となる範囲を求めてみよ。図示するのも良い。
こちら大学で出されたんですが、解説できますか?
あ、コメントありがとうございます!いつもスパムばかりだし、コメントが来たらメールで送るとかいう設定もしていないので、今偶然見ました。考えてみるのでちょっと待ってくださいね。
あらためまして。簡単です。正しい値に対して、正しい値からの誤差が1%であるという意味の式、すなわち、\[ { ( I(\nu)_{plunk} – I(\nu)_{Rayleigh} ) / I(\nu)_{plunk} } < 1/100 \] という不等式を解けばいいだけですよ。 両 \( I(\nu) \) の表式と、\( T=5000 \) を代入して。そうすると、振動数が大きい(波長が短い)ところではレイリージーンズの式は正しい答えからずれるという結果がでて、この結果は、波長が短いところでは量子論的な効果が卓越するので、古典論で考えたものであるレイリージーンズの式は破綻する、と考察することできる、ということになるのですよね。