【量子力学】角運動量の合成とクレブシュゴルダン係数
例えば、2つの スピン \( s=5/2 \) の同種の粒子 \( A , B \) があって、\( A \) のスピンの \( z \) 成分が \( s_{Az} =5/2 \) つまり純粋な上向き、\( B \) は \( s_{Bz}=3/2 \) であるとして、これら2つの粒子が1つの複合粒子を作るとき、この複合粒子のスピンを計ったらどうなるか、スピンを合成したらどうなるのか、というのがここで扱う問題です。また、例えば水素原子核の周りをまわっている電子は、軌道角運動量とスピンの両方を持っていますが、この軌道角運動量とスピンの2つを合成する場合も、どうように扱うことができます。
なお、本記事では スピン \( (1/2) \hbar \) を単に \( 1/2 \) のようにあらわします。すなわち、\( \hbar \) を省略します。
複合粒子のスピンを計るには例えば 複合粒子が磁場中を過ぎ去るときの磁場との相互作用をみればいいわけで、複合粒子は 全スピン \( S (やs) \) と その \( z \) 成分 \( S_z(やs_z) \) をもつ一つの粒子として磁場と相互作用し、観測されるわけです。
合成というなら、\( A \) のスピン \( |5/2, \ \ 5/2 \rangle_A \) と \( B \) のスピン \( |5/2, \ \ 3/2\rangle_B \) を足すんだから、\( j = 5/2 + 5/2 = 5 , m = 5/2 + 3/2 = 4 \) でいいじゃないか、というのは簡単な考察ですが、そうはいきません。
古典力学的に角運動量の合成を考えるならば、これは単純に 粒子\( A \) と 粒子\( B \) の角運動量ベクトル(スピンのベクトル)を足し合わせて、下図のように幾何学的に \( S^2 = S_x^2 + S_z^2 \) と \( S_z = S_{1z} + S_{2z} \) とすれば合成と言わずとも単に角運動量の和として値が確定しますが、量子力学では角運動量の2つの成分は同時に確定できないから三平方の定理によって幾何学的に考えられないし、さらに成分もとびとびの値しかとれないという制約があるからなお困難で古典力学のようにはいかず、量子力学的に考える必要があるわけです。ただ、磁気量子数つまり、角運動量の \( z \) 成分 \( m \) は \( z \) 方向のものと決まっているので、\( m = m1+ m2 \) のように単純な足し合わせが利きます。一方、全角運動量量子数 \( j = j1 + j2 \) は必ずしも成り立ちません。磁気量子数がなぜ磁気量子数というのか、それは磁場をかけたときに観測される量子数だからですね。
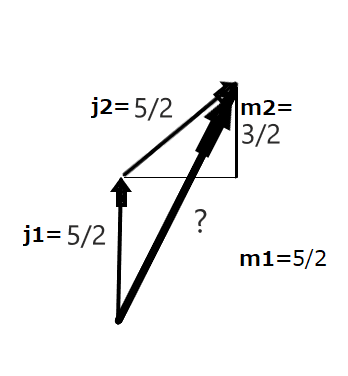
さて、結果から言うと、角運動量の合成の方法により計算すると、上で述べた 2 つの粒子が作る複合粒子のスピンの状態を \( |5/2, \ 5/2 \rangle_A |5/2,\ 3/2\rangle_B \) と表したとき、この \( |5/2, \ 5/2\rangle_A |5/2, \ 3/2\rangle_B \) は \( |5/2, \ 5/2\rangle_A |5/2, \ 3/2\rangle_B = (|5, \ 4\rangle – |4, \ 4\rangle)/\sqrt{2} \) と表すことができることがわかります。これは、この複合粒子が観測されるとき、\( s=5 \) かつ \( s_z = 4 \) の粒子であると観測される場合と、\( s = 4 \) で \( s_z = 4 \) の粒子であると観測される場合の2つの場合が(係数の比較により、等確率で)あることを示しています。\( |4, \ 4\rangle \) が観測されてしまうとそのときは \( 5/2 + 5/2 \neq 4 \) なので \( j = j1 + j2 \) が成り立たないことがわかります。角運動量の合成を系統的に行えば、例えば上記でもわかるように、\( |5, \ 4\rangle \) が何%、\( |4, \ 4\rangle \) が何%で観測されたという実験結果により、それを構成する2つの、あるいは複数のそれぞれの粒子の状態はどのような確率でこうである、ということもわかってしまうのです。どんな粒子であるかのあたりがつくこともあるでしょう。だから角運動量の合成は粒子の構成を調べる上で非常に役に立つ理論です(なはずです。知らない^^)
一方、2つのスピン \( 5/2 \) の粒子 \( A,\ B \) の複合粒子が一つの粒子として、\( s=5, s_z= 4 \) の確定した状態 \( |5, \ 4\rangle \) である(と観測された)とき、
\begin{eqnarray*} |5 \ 4\rangle &=& (1/\sqrt{2})|5/2, \ 3/2\rangle_A |5/2, \ 5/2\rangle_B \\ &+& (1/\sqrt{2})|5/2, \ 5/2\rangle_A |5/2, \ 3/2\rangle_B \end{eqnarray*} と表されることも角運動量の合成の計算からわかります。これは、複合粒子が \(|5, \ 4\rangle \) の状態として計測された時の \( A,\ B \) の各粒子のスピンの状態は、\( A \) のスピンが \( s_{Az} = 3/2 \) で \( B \) のスピンが \( s_{Bz} = 5/2 \) である場合と、 \( A \) のスピンが \( s_{Az} = 5/2 \) で \( B \) のスピンが \( s_{Bz} = 3/2 \) である場合の2つの場合が(等確率で)ある(観測される)ということを示しています。こういう観測結果は量子力学的です。
角運動量の合成のやりかたによると、まず後者の \(|j, \ m\rangle \) を 基底 \(|j1, \ m1\rangle |j2, \ m2\rangle \) で展開する方法が得られ、それから逆算して前者の、\( |j1, \ m1\rangle |j2, \ m2\rangle \) を \(|j, \ m\rangle \) で表す方法が得られます。前もって言っておくと、一般的には \( j, m \) の整数値が与えられるたときに \( j, m \) を公式に当てはめて係数が得られるというものではありません。
角運動量の合成の方法はどのような量子力学的な扱いが必要な粒子にたいしても適用できます。古典力学で角運動量の加算が、地球と火星だろうが ひもにつながれて回っているパチンコ玉だろうが関係なく行えるように、量子力学の角運動量の合成の理屈も粒子の種類に依存せず角運動量の量子数というもののみを介してどんな粒子にも成り立ちます。また、角運動量の合成は、軌道角運動量 \( S \) に対しても スピン \( s \) に対しても同じ扱いで行うことができます。
簡易版を用意しました。簡易版はこちら。
では、角運動量の合成の方法をみてみましょう。
角運動量を合成する2つの粒子 \( A \), \( B \) のそれぞれの角運動量の状態は、\(|j1, \ m1\rangle \) と \(|j2, \ m2\rangle \) で表します。2つの粒子の角運動量を合成した状態、つまり複合粒子の 角運動量の状態は \(|j1, \ m1\rangle |j2, \ m2\rangle \) のようにあらわすことができます。これは、\(|j1, \ m1\rangle \)かつ\(|j2, \ m2\rangle \) ということを表しています。一般的な合成角運動量の状態は、後述するように \( (2j1+1)(2j2+1) \) 個の \(|j1, \ m1\rangle |j2, \ m2\rangle \) の線形結合で表されます。また、\(|j1, \ m1\rangle_A |j2, \ m2\rangle_B \) のようには書かないことにします。なぜなら、\( j1 \) や \( j2 \) の \( 1 \) や \( 2 \) で \( A \)、\( B \) どちらの粒子なのかを判別できるからです。もちろん \( j1 \) は \( A \) の、\( j2 \) は \( B \) の全角運動量量子数です。
これ以降、\( m1 \) は \( -j1 \leq m1 \leq j1 \) によって \( 2j1 + 1 \) 個の値の間を動きますが、\( j1 \) は変化しません。例えばスピン \( 5/2 \) の粒子を扱うのであれば \( j1 = 5/2 \) ということであり、この \( j1 \) は 合成の手順の間変化することはありません。\( m2, j2 \) についても全く同様です。これ以降、\( m1 \) を \( 1 \) 増やしたり、 \( m= m1 + m2 \) である \( m \) が \( 1 \) ずつ減ったりとちみちみいろいろ動きますが、手順の間、\( m1, m2 \) は変化するのに対し、\( j1, j2 \) はそれぞれ変化しない一つの値を表します。\( j1 \) や \( j2 \) はそれぞれの粒子の全角運動量の大きさであり、変化しません。対して \( z \) 方向成分である \( m1, m2 \) は全角運動量の方向によって変わるので、変化します。角運動量の合成とは、2つの粒子の角運動量が衝突などによりやりとりされる中での、角運動量保存のようなものとは違います。
ということで \( m1 \) は \( -j1 \) と \( j1 \) の間の \( 2j1+1 \) 個の値、\( m2 \) は \( -j2 \) と \( j2 \) の間の \( 2j2+1 \) 個の値の間を動くので、\(|j1, \ m1\rangle |j2, \ m2\rangle \)で表される複合粒子の角運動量の基底状態は \( (2j1+1)(2j2+1) \) 個あることになります。これら \( (2j1+1)(2j2+1) \) 個の状態は \( j1 \) や \( m1 \) の固有状態ですが、基底状態と書いたのは、複合粒子の角運動量の状態が、これらの線形結合で表されるからです。観測され得る個々の状態は \( (2j1+1)(2j2+1) \) 個でも、複合粒子の合成された角運動量の状態というのはそれら個々の状態がどれくらいの割合で観測できるかで決まってくるので、それを「角運動量の状態」というわけで、それはそれら\( (2j1+1)(2j2+1) \) 個の基底状態の線形結合であらわされます。
粒子 \( A \) と粒子 \( B \) の状態の組で、とりうる観測可能なすべての組み合わせは \( (2j1+1)(2j2+1) \) 個でありこれ以外の組というものは存在しません。そして、各組にたいして何%の確率で出現するかの重みをかけたそれらの線形結合で、複合粒子のすべての角運動量の状態を表すことができるから、複合状態の角運動量状態空間の次元は\( (2j1+1)(2j2+2) \) であるということができます。
合成系の角運動量演算子 \( \hat{j} \) は 粒子 \( A \) の角運動量演算子 \( \hat{j1} \) と 粒子 \( B \) の角運動量演算子 \( \hat{j2} \) に対して \( \hat{j} = \hat{j1} + \hat{j2} \) で定義されますが、これはベクトル演算子です。だから、\( j \) は、\( j = j1 + j2 \) のような単純な和にはなりません。
角運動量の合成の計算にだんだん近づいていきます。
2つの粒子の全角運動量をそれぞれ、\( j1, j2 \) とし、2つの粒子の角運動量の状態 \( |j1, \ m1\rangle \) と \(|j2, \ m2\rangle \) を合成します。\( \vec{\hat{j}} = \vec{\hat{j1}} + \vec{\hat{j2}} \) だったから、\( \hat{j_z} = \hat{j1_z} + \hat{j2_z} \) 。
あらかじめ言っておくと、合成系について調べるには、例えば、2つのスピン \( 5/2 \) の粒子の合成系の \(|4, \ 4\rangle \) について知りたいときでも、係数を求めるには、\(|5, \ 5\rangle = |5/2, \ 5/2\rangle_A |5/2, \ 5/2\rangle_B \) から調べていかなくてはいけません。さて、
\begin{eqnarray*} \hat{j_z}|j1, \ m1\rangle |j2, \ m2\rangle &=& (\hat{j1_z} + \hat{j2_z} )|j1, \ m1\rangle |j2, \ m2\rangle \\ &=& (m1 + m2)|j1, \ m1\rangle |j2, \ m2\rangle \end{eqnarray*} だから、合成系 \( |j1, \ m1\rangle |j2, \ m2\rangle \) は \( \hat{j_z} \) の 固有値 \( m = m1 + m2 \) の固有ベクトルです。角運動量の \( z \) 成分が足せるというのはこのような根拠によります。
ここからが、角運動量の合成の仕方です。
角運動量の合成の具体的な計算
さて、まず合成系で、粒子 \( A \) の \( m1 \) と 粒子 \( B \) の \( m2 \) がともにそれぞれ最大値 \( j1 \) と \( j2 \) である場合を考えます。このときの合成系のスピンの状態は \( |j,\ m\rangle = |j1,\ j1\rangle |j2,\ j2\rangle \) と書けます。
角運動量の \( z \) 成分同志は足し算ができるので、\( m = m1 + m2 = j1 + j2 \) となります。\( j = j1 + j2 \) はまだ明らかなようで明らかではありません。しかし、角運動量の一般論から、角運動量状態空間の中で、ある状態が、それ以上の \( m \) の状態が存在しないような状態である場合、そのような 状態は \( j^2 \) の、\( j = j1 + j2 \) のときの固有値 \( j(j+1) \) の固有状態であるということがいえるので、\( m = j1+j2 \) はこの合成系としては最大値でこれ以上の値が存在しないことから、結果として、\( j = j1 + j2 \) が言えます。つまり、\( |j1+j2,\ j1+j2\rangle = |j1,\ j1\rangle |j2,\ j2\rangle \) です。
これ以降、「\(j^2 \) の \( j=j1+j2 \) のときの固有値 \( j(j+1) \) の固有状態」などを、単に、\( j^2\) の \( j=j1+j2 \) の固有状態、などと言います。
この、\(|j1+j2,\ j1+j2\rangle = |j1 \ j1\rangle |j2 \ j2\rangle \) に対して下降演算子 \( \hat{j^-} = \hat{j1^-} + \hat{j2^-} \) を作用させていきます。
\( \hat{j^-} \) は 状態の \( m \) を、\( \hat{j1^-} \) は 状態の \( m1 \) を、\( \hat{j2^-} \) は 状態の \( m2 \) を それぞれ \( 1 \) 減らす演算子です。\( \hat{j1^-} \) や \( \hat{j2^-} \) が、\( j1 \) や \( j2 \) を減らすものでないことに注意してください。\( j1 \) や \( j2 \) は変化しません ! \( j \) は変化します。
下降演算子が \( \hat{j^-} = \hat{j1^-} + \hat{j2^-} \) である理由は、簡単ですが、おまけに示します。
下降演算子を作用させると、\begin{eqnarray*} \hat{j^-} |j1+j2, \ j1+j2\rangle &=& (\hat{j1^-} + \hat{j2^-} )|j1 \ j1\rangle |j2 \ j2\rangle \\ &=& \hat{j1^-} |j1,\ j1\rangle |j2,\ j2\rangle \\ &+& \hat{j2^-} |j1,\ j1\rangle |j2,\ j2\rangle \end{eqnarray*}
より、
\begin{eqnarray*} |j1+j2,\ j1+j2-1\rangle &=& |j1, j1-1\rangle |j2, j2\rangle \\ &+& |j1, j1\rangle |j2, j2-1\rangle \ \ … (1) \end{eqnarray*} を得ますが、
これにまた下降演算子を作用させるということを繰り返すと、
\begin{eqnarray*} |j1&+&j2,\ j1+j2\rangle \\ |j1&+&j2,\ j1+j2-1\rangle \\ |j1&+&j2,\ j1+j2-2\rangle \\ &…& \\ |j1&+&j2,\ -(j1+j2)\rangle \end{eqnarray*}
までの 計 \( 2(j1+j2) + 1 \) 個の状態を得ることができます。\( j \) は変化させていないので、これら \( 2(j1+j2) + 1 \) 個はすべて \( j^2 \) の \( j = j1+j2 \) の固有状態であり、また \( j^2 \) の \( j=j1+j2 \) の固有状態はこれですべてです。
これはスピン \( 5/2 \) の2つの粒子の合成の場合で言えば、\( |5,\ 5\rangle, |5,\ 4\rangle, |5,\ 3\rangle, … ,|5,\ -5\rangle \) までの \( 2 \times (5/2+5/2) + 1 = 11 \) 個の状態について角運動量の合成ができたことを示しています。
\begin{eqnarray*} |5,\ 5\rangle &=&|5/2,\ 5/2\rangle |5/2,\ 5/2\rangle \\ |5,\ 4\rangle &=&|5/2,\ 3/2\rangle |5/2,\ 5/2\rangle + |5/2,\ 5/2\rangle |5/2,\ 3/2\rangle \\ |5,\ 3\rangle &=& |5/2,\ 1/2\rangle |5/2,\ 5/2\rangle + 2 |5/2,\ 3/2\rangle |5/2,\ 3/2\rangle \\ +&& |5/2,\ 5/2\rangle |5/2,\ 1/2\rangle \\ &…& \end{eqnarray*}
こうして \( j= j1+j2 \) の状態について求めることができたので、次は \( j=j1+j2-1 \)、つまり例でいえば \( j=4 \) について求めたい。つまり \(|4,\ 4\rangle \) から再びさきのような 下降演算子の演算を行い \( |4,\ 3\rangle,\ |4,\ 2\rangle … \) が求められれば角運動量の合成の計算を続けられそうです。
そのために、次に、はじめの、\( (2j1+1)(2j2+1) \) 個の基底で張られる角運動量状態の全空間から、今求めた、これら \( 2(j1+j2) +1 \) 個の基底で張られる部分空間を除いてみます。これは、はじめの空間から \( j^2 \) の、\( j=j1+j2 \) の固有状態をすべて取り除いたことになります。
取り除いた結果、\( m \) が唯一最大の状態であった \(|j1+j2,\ j1+j2\rangle \) が取り除かれ、\( |j1+j2,\ j1+j2-1\rangle \) も取り除かれたから、残りの空間における \( m=j1+j2-1 \) の部分空間の次元は一つ減り…といきたいのですが、\( m \) で区別される \( m \) ごとの部分空間について調べるために、\( m \) ごとに、縮退度(多重度)を調べます。部分空間とは、例えば \( m=j1+j2-1 \) の部分空間といったら、\( m \) が \( j1+j2-1 \) であるような状態の集まりということで、1つ以上の基底(固有状態)があり、その基底の線形結合で表されます。
多重度を、\( m \) の最大値 \( j1+j2 \) からはじめて調べていきます。
\( \hat{j_z} \) の最大固有値は \( m= m1 + m2 \) の最大値であり、それを与えるのは \( m1 \) と \( m2 \) がともに最大となるとき、つまり \( m1=j1, m2=j2 \) のときで、そのとき \( m= j1 + j2 \) となります。\( m=j1+j2 \) を与える状態は、\( (2j1+1)(2j2+1) \) 個の \( |j1,\ m1\rangle |j2,\ m2\rangle \) の固有状態(基底)の中で \( |j1 \ j1\rangle |j2 \ j2\rangle \) の1個だけです。つまり \( \hat{j_z} \) の固有値 \( m = j1 + j2 \) の状態の多重度(次元) = \( 1 \)。
次にいきます。\( \hat{j_z} \) の \( m = j1 + j2 \) より一つ小さい固有値は、\( m = j1 + j2 – 1 \) です。この固有値を与える状態は、\( m1 = j1, m2 = j2 – 1 \) の場合と、\( m1 = j1 -1, m2 = j2 \) の場合の2つ、つまり \(| j1 \ j1\rangle |j2 \ j2-1\rangle \) と \(|j1, \ j1-1\rangle |j2, \ j2\rangle \) の2つです。両方の場合で、確かに \( m= m1+m2 = j1+j2-1 \) となりますね。この2つの状態のうちの前の状態、つまり、\( m1 \) が \( j1 \) で \( m2 \) が \( j2-1 \) であるとき、後ろの状態である \( m1 \) が \( j1-1 \) で \( m2 \) が \( j2 \) の状態となることは絶対にないので、この2つは独立です。あるいは直交しています。この2つの状態は、\( j^2 \) の固有状態ではありません。そして、数えてみても、\( m = j1+j2 -1 \) を満たす固有状態はこの独立な2つの状態しかありません。
つまり、\( \hat{j_z} \) の固有値 \( m = j1 + j2 – 1 \) の状態の多重度は 2 となります。そして、\( m=j1+j2-1 \) のすべての状態はこれら2つの状態、\(| j1 \ j1\rangle |j2 \ j2-1\rangle \) と \(|j1, \ j1-1\rangle |j2, \ j2\rangle \) の線形結合で表され、それらの状態のなす部分空間の次元は2。\( \hat{j_z} \) の固有値 \( m = j1 + j2 – 1 \) は縮退度2 に縮退しています。
そして次、\( m = j1 + j2 – 2 \) の場合は多重度は3。\( (m1,\ m2) = (j1-2,\ j2),\ (j1-1,\ j2-1),\ (j1,\ j2-2) \) の3つの基底。
こうしていくと、
\begin{array}{|l|c|} \hline j の 固有値 & 多重度(縮退度、次元) \\ \hline j1+j2 & 1 \\ j1+j2 – 1 & 2 \\ j1+j2 – 2 & 3 \\ … & … \\ |j1-j2| & j1+j2+1-|j1-j2| \\ … & … \\ -(j1+j2-1) & 2 \\ -(j1+j2) & 1 \\ \hline \end{array}
…となります。イメージだけつかめれば個数自体は関係ありません。この上から下に向かて \(1 \)、\( 2 \)、\( 3 \)と順次増えていきまた減少に転じて最後は位置になるという、上の方がピラミッド型の縮退度の様子だけわかれば。
数え方は複雑になりそうですが、図で見るとすっきりします。それはおまけにまわします。
ということで話をもどして、角運動量状態の全空間から、\( j=j1+j2 \) の \( 2(j1+j2)+1 \) 個の基底を取り除くことを考えます。
まず、はじめの \( (2j1+1)(2j2+1 ) \) 個の基底のなす空間から、基底 \( |j1+j2,\ j1+j2\rangle \) を取り除くと、これは唯一の \( m \) が最大(\(=j1+j2\) ) の基底だったので、残った空間には \( m = j1+j2 \) の 状態はなくなり、残りの空間では \( m = j1+j2-1 \) が最大になります。
多重度のはなしで、\( m \) が次に大きい \( m=j1+j2-1 \) の多重度は \( 2 \) でしたが、これは \( \hat{j_z} \) の固有値 \( m=j1+j2-1 \) の状態の集合をなす部分空間が \( 2 \) 次元であることを表しています。そこで、次に取り除きたい \( |j1+j2,\ j1+j2-1\rangle \) を取り除くと、残りの空間では \( m=j1+j2-1 \) の部分空間の次元は \( 1 \) になります。
さきに \( m=j1+j2-1 \) の多重度・次元が\( 2\) であると述べた時のその2次元を表す基底とは、
\(| j1, \ j1\rangle |j2, \ j2-1\rangle \) と \(|j1, \ j1-1\rangle |j2, \ j2\rangle \) の2つでした。これを \( e_1,\ e_2 \) とします。それに対し、今取り除きたい \( |j1+j2,\ j1+j2-1\rangle \) は、もうかなり前の (1) の計算の結果、\(| j1, \ j1\rangle |j2, \ j2-1\rangle + |j1, \ j1-1\rangle |j2, \ j2\rangle \) とあるようにこれは、\( e_1+e_2 \) です。
では、\( m=j1+j2-1 \) の部分空間の基底は、多重度の話からは \( e_1, e_2 \) であるということでしたが、その部分空間から基底 \( e_1+e_2 \) を取り除くとは、どういうことかというと、これは、\( e_1, e_2 \) の基底で表される空間を別の基底、\( e_1+e_2 \) と それに直交する 基底 \( e’\ \) で表すことにして、それから \( e_1+e_2 \) を取り除くということになります。したがって残りの空間には基底 \( e’\ \) が残ります。\( e’\ \) はベクトル代数の計算から \( e_1-e_2 \) と計算できます。残りの空間の中の \( m=j1+j2-1 \) の部分空間は \( e’\ \) 1つが支える次元\(1\) の空間です。
\( e_1-e_2 \) は \( m=j1+j2-1 \) の部分空間の基底なので、( \( j \) でもいいのですが) 未知ということで \( x \) を用いて、\( e_1-e_2 = |x,\ j1+j2-1\rangle \) と表すことができます。ところが、この残りの空間の中で、\( m=j1+j2-1 \) は最大の値であり(※)、それ以上の \( m \) の状態が存在しないことから、再び一般論で、そのような 状態は \( j^2 \) の \( j=j1+j2-1 \) の固有状態であるということができるから、\( x=j1+j2-1 \) であるということになります。具体例でいえば、\( e_1-e_2 = |4,\ 4\rangle \) ということが言えたのです。さきほど欲しかった \( |4,\ 4\rangle \) が \( |5/2,\ 3/2\rangle |5/2,\ 5/2\rangle – |5/2,\ 3/2\rangle – |5/2,\ 5/2\rangle \) として得られました(ただし正確には \(1/\sqrt{2} \)倍してください)。そこでまた下降演算子によって \begin{eqnarray*} |j1&+&j2-1,\ j1+j2-1\rangle \\ |j1&+&j2-1,\ j1+j2-2\rangle \\ &…& \\ |j1&+&j2-1,\ -(j1+j2-1) \rangle \end{eqnarray*} の \( (j1+j2-1)\times 2 – 1 \) 個の状態が得られることになります。ここでのポイントは、\( |\color{magenta}{j1+j2},\ j1+j2-1\rangle \) に直交する状態として、\( |\color{magenta}{j1+j2-1},\ j1+j2-1\rangle \) が得られるということです。こうして、具体例でいえば、
\(|5,\ 5\rangle \) から下降演算子を用いて計算し、 \(|5,\ 4\rangle \) に直交する状態として \(|4,\ 4\rangle \) を得、そこからまた下降演算子で計算し、\(|4,\ 3\rangle \) に直交する状態として \(|3,\ 3\rangle \) を得、そこから、下降演算子、と繰り返すと、すべての \(|j,\ m\rangle \) の \(|j1,\ m1\rangle |j2,\ m2\rangle \) による表現を得ることができます。直交する状態を得る部分に関しては、取り除いた状態が、\( e_1+e_2 \) の形とは限らないし、したがって直交する基底が \( e_1-e_2 \) になるとも限りません。また、例えばですが、\( |3,\ 3\rangle \) を求めようとして、\( |4,\ 3\rangle \) に直交する基底を求めようとしたが任意性により決定できないときに、\(|5,\ 3\rangle \) にも直交するという条件を用いて決定するというような場合もあります。\( m \) が同じで \( j \) の異なる ある \( m \) の部分空間の基底 \(|5,\ 3\rangle,\ |4,\ 3\rangle,\ |3,\ 3\rangle \) はすべて互いに直交するのです。というか、すべての \(|j,\ m\rangle \) は独立に観測されるものであり、直交します。\( |j1,\ m1\rangle |j2,\ m2\rangle \) もすべて独立で、直交します。
また、\( e_1, e_2 \) それぞれは \( \hat{j_z} \) の固有ベクトルではあっても \( j^2 \) の固有ベクトルではありませんでしたが、下降演算子によって得られ、そして取り除かれた \( e_1+e_2 \) は \( \hat{j_z} \) の固有ベクトルでかつ \( j^2 \) の固有ベクトルでもありました。さらにそれに直交する \( e_1-e_2 \) も \( j^2 \) の固有状態だったのです。今までやったことは、\( j^2 \) の固有ベクトルを求めて行った対角化というものです。
こうして、順次求めると、\( |j,\ m>=\Sigma C_{j1,m1,j2,m2}^{j,m} |j1,\ m1\rangle |j2,\ m2\rangle \) と表すことができ、そのときの \( C_{j1,m1,j2,m2}^{j,m} \)のことをクレブシュゴルダン係数と言います。
角運動量の合成、あるいはクレブシュゴルダン係数の計算例
例えば、先にも書いた、\(|5,\ 4\rangle \) を求めたくても、2つの粒子のスピンや角運動量が定まらないとわかりません。\( |4,\ 4\rangle \) を求めるときでも、\(|5,\ 5\rangle \) から順次下降演算子を作用させて求めていかなくてはなりません。
スピン \( 3/2 \) と 角運動量 \( 1 \) の合成系 \( \sim \) スピンも軌道角運動量も同じく扱えます。
\(|3/2,\ 3/2\rangle |1,\ 1\rangle = |5/2, 5/2 \rangle \) から始めます。
\begin{eqnarray*} |5/2,\ \ \ 5/2\rangle &=& |3/2,\ 3/2\rangle|1,\ 1\rangle \\ | 5/2,\ \ \ 3/2\rangle &=& |3/2,\ 1/2\rangle |1,\ 1\rangle + |3/2,\ 3/2\rangle |1,\ 0\rangle \ \ (= e_1 + e_2 にあたるもの) \\ |5/2,\ \ \ 1/2\rangle &=& |3/2, -1/2\rangle |1, 1\rangle + 2|3/2,\ 1/2\rangle |1,\ 0\rangle + |3/2,\ 3/2\rangle|1, -1\rangle \\ |5/2,-1/2\rangle &=& |3/2, -3/2\rangle |1,\ 1\rangle + 3|3/2, -1/2\rangle |1,\ 0\rangle + 3|3/2,\ 1/2\rangle |1, -1\rangle \\ |5/2, -3/2\rangle &=& 4|3/2, -3/2\rangle|1,\ 0\rangle + 6|3/2, -1/2\rangle |1, -1\rangle \\ |5/2, -5/2\rangle &=& 10 |3/2, -3/2\rangle |1, -1\rangle \end{eqnarray*}
\begin{eqnarray*} |3/2,\ \ \ 3/2\rangle &=& |3/2,\ 1/2\rangle |1,\ 1\rangle – |3/2,\ 3/2\rangle |1,\ 0\rangle \ \ (= e_1 – e_2 にあたるもの) \\ |3/2,\ \ \ 1/2\rangle &=& |3/2, -1/2\rangle |1,\ 1\rangle – |3/2,\ 3/2\rangle |1, -1\rangle \\ |3/2, -1/2\rangle &=& |3/2, -3/2\rangle |1,\ 1\rangle + |3/2, -1/2\rangle |1,\ 0\rangle – |3/2,\ 1/2\rangle|1, -1\rangle \\ |3/2, -3/2\rangle &=& 2|3/2, -3/2\rangle |1,\ 0\rangle \end{eqnarray*}
\begin{eqnarray*} |1/2,\ \ \ 1/2\rangle &=& |3/2, -1/2\rangle |1,\ 1\rangle + |3/2,\ 3/2\rangle |1, -1\rangle \\ |1/2,-1/2\rangle &=& |3/2,-3/2\rangle|1, 1\rangle + |3/2,-1/2\rangle |1,\ 0 \rangle + |3/2,\ 1/2\rangle |1, -1\rangle \end{eqnarray*}
おまけ:\( \hat{j^-} = \hat{j1^-} + \hat{j2^-} \) の証明
\( \vec{\hat{j}} = \vec{\hat{j1}}+\vec{\hat{j2}} \ \ \ \to \ \ \hat{j_{x(yz)}} = \hat{j1_{x(yz)}} + \hat{j2_{x(yz)}} \\ \hat{j1^-} = \hat{j1_x} – i\ \hat{j1_y} ,\ \ \hat{j2^-} = \hat{j2_x} – i\ \hat{j2_y} \) より \( \hat{j^-} = \hat{j_x}-i\ \hat{j_y} = \hat{j1_x}+\hat{j2_x} – i(\hat{j1_y}+\hat{j2_y}) = \hat{j1^-} + \hat{j2^-} \)
おまけ:多重度の数え方。
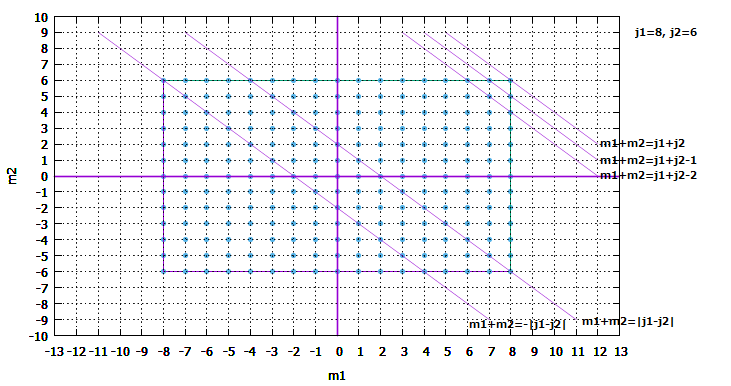
多重度を数えるとはいったい何をやっているかというと、\( m1+m2= m ( -(j1+j2) \le j \le j1+j2) \) を満たす \( m1 \) と \( m2 \) の組で、\( m1 \) が \( -j1 \le m1 \le j1 \)、\( m2 \) が \( -j2 \le m2 \le j2 \) を満たすものの数を数えることであって(それが多重度)、図で整理すれば、下図の \( m1+m2 = m \) の各直線上の格子点のうち、長方形の領域の中にあるものの数を数えればいいことになり、これで見通しがよくなりました。\( m = j1+j2 \) からはじめて、\( m = j1+j2-1,\ m = j1+j2-2 \) … というふうに調べていけばいいことになります。
すると、長方形が縦長になる場合も含めて、\( |j1-j2| \lt m \le j1+j2 \) のときは、多重度は \( (j1+j2) – m + 1 \) となり、つまり、\( m \) は 一つ減るごとに 多重度は \( 1 \) ずつ増えていき、\( -|j1-j2| \le m \le |j1-j2| \) のときは、点の数つまり多重度は \( j1+j2-|j1-j2| + 1 \) で増減せず一定で、 \( -(j1+j2) \le m \lt -|j1+j2| \) の間は、 多重度は \( (j1+j2) + m + 1 \) となり、 \( m \) が減るごとに \( 1 \) ずつ減っていくこととなります。
さらにおまけとしては、角運動量の合成の計算の結果、はじめの \( (2j1+1)(2j2+1) \) 個の基底で表されていた空間を、\( j=j1+j2 \) の \( (j1+j2) \times 2 + 1 \) 個の基底、\( j= j1+j2+1 \) の \( (j1+j2-1) \times 2 + 1 \) 個の基底、\(j=j1+j2-2 \) の \( (j1+j2-2) \times 2 +1 \) 個の基底、と基底を変えて表すことができたのですが、基底を変えてもその基底の数は、\( (2j1+1)(2j2+1) \) 個であることが、簡単な和の計算により、証明できます。
\begin{eqnarray*} (2j1+1)(2j2+1 ) &=& \{ (j1+j2) \times 2 + 1 \} \\ &+& \{ (j1+j2-1) \times 2 + 1 \} \\ &+& … \end{eqnarray*}
これを、具体的な数字を用いれば、
\[ 6 \otimes 6 = 11 \oplus 9 \oplus 7 \oplus 5 \oplus 3 \oplus 1 \ \ … (2) \]
のようにあらわし、直積空間 \( |j1,\ m1\rangle |j2,\ m2\rangle \) の既約分解といいます。
(2) 式では \( \otimes \) を \( \times \)、\( \oplus \) を \( + \) に読みかえれば、普通の数字の等式として成り立っていることがわかります。
以上、角運動量の合成について述べました!
でも僕は思うんです。角運動量の合成のところで、量子力学的に特別などんなきまりを使っているかと考えると、数が離散的なことと、足し算と、ベクトルだけじゃないですか、とくに量子力学だからっていうものを、離散的というのはそうだけど、特に感じない。角運動量の成分を三平方の定理などをつかって幾何学的にきっちり表すことができないから、ベクトルを使ってそれに準ずることをしている。
それだけのことから、複合粒子を観測した場合の、複数の状態のそれぞれの現れる確率、自然の従う法則を計算できるっていうのは、なんかすごく不思議だと思うんです。あるいは逆に、単にやはり、角運動量の合成なんて、単なるランダムの問題の確率論に過ぎない、という感覚もでてきますよね(そうではないと思っていますけど)。


ディスカッション
コメント一覧
まだ、コメントがありません