【天文学】古代人の叡智～地球の周の長さを求め、最後には太陽の大きさを知る
■地球の周の長さ(半径)を求める
■月の大きさを求める
■月までの距離を求める
■太陽までの距離を求める
■太陽の大きさを求める
これらは、上からこの順序で、芋づる式に求めることができます。もちろん必要な測定(観測)を行う必要がありますが。一文で説明すると、地球の周の大きさを求めると、次に月の大きさを求めることができて、そうすると次に月までの距離を求めることができ、さらには太陽までの距離、太陽の大きさと、順次求めることができる、ということです。
古代ギリシャ、紀元前\(200\)年。この時代に、地球の大きさを計算できたのは驚きです。そしてさらそこから、月の大きさ、月までの距離、太陽までの距離、太陽の大きさ、そんなことまでわかってしまうのです。神話の世界はもっと前の時代のものですが、天上の世界は別世界だと思われていたし、地球球体説はあったものの、地球が丸いことが証明されているわけでもなかった。地球が丸いと実証できたのは世界一周が成し遂げられた16世紀なのであって、地球が丸いという地球球体説というもの自体まだまだ想像上のことで、実感のない事実だったことでしょう。それなのに地球の大きさを求めた。
地球の大きさ、月の大きさ、月までの距離、太陽までの距離、太陽の大きさ、これらは、この順序で、芋づる式に求めることができます。これを求めたのが、紀元前\(200\)年のエラトステネスです。これらを求めるにあたり実測しなければいけないもので手間がかかるのは、シエネという場所からアレクサンドリアという場所までの距離で、エラトステネスはこの距離を当時すでに知られていた情報として使ったのでしょうが、これは歩いて測るしかなかったでしょう。しかし、そのほかに必要な数字は、分度器と時計(当時のことだから砂時計か水時計)で測れるものです。それだけ実測すれば、地球の大きさから太陽の大きさまでを計算できるのです。すばらしい！このエラトステネスの話は、宇宙論を扱う本でしばしば登場します。
では、地球の大きさをどうやって求めるのか、から説明していきましょう。
地球の周の長さを求める
シエネとアレクサンドリアの距離を測ってから、アレクサンドリアで一本の棒を立てれば地球の一周の長さがわかる！？
エラトステネスが地球の大きさを測るにあたり利用したのは、(夏至の日の正午)シエネという場所で、太陽が真上に来る、という事実でした。シエネの井戸の底から空を見上げると夏至の日の正午に太陽が真上に見えたそうです。その真北(つまり同じ経度上の北)のアレクサンドリアでは、同じ時刻の太陽の位置は、真上ではありません。地面に垂直に棒を立てると、棒は太陽光線とある角度をなします。棒は地面に垂直に立てます。また、シエネとアレクサンドリアの距離は、この時代実際に歩いて測った結果があったと思われますが、当時は\(920km\) とされていました。実際には\(800km\) 程度で、こちら数字を使えばこれから求められる値より正しい地球の大きさが求まります。さて、夏至の日の正午のこれらのことを図示すると以下のようになります。
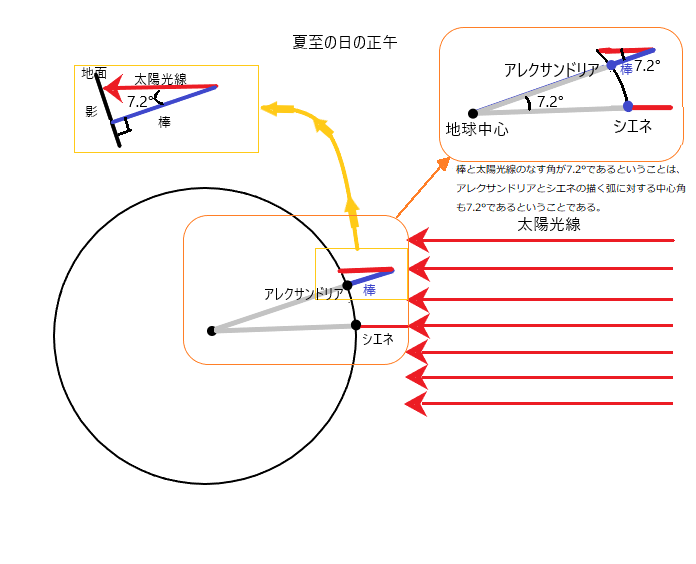
まず手っ取り早く説明すると、アレクサンドリアで地面に垂直にたてた棒と太陽光線のなす角度を測ると(影を測る)、\( 7.2^\circ \) なので、アレクサンドリアとシエネの弧が地球中心に対してなす角も \( 7.2^\circ \) だということになるから、アレクサンドリアとシエネの距離さえ測れば、地球一周の長さが(地球の半径も)計算できる、ということになります。
図は、アレクサンドリアで、夏至の日の正午、地面に垂直に棒を立て、そこに太陽光線があたっている様子を表しています。(夏至の正午に)アレクサンドリアで地面に垂直に立てた棒をまっすぐ地球の中の方向に伸ばしていけば、地面に垂直に棒を立てたわけだからそれは地球の真ん中(中心)に達します。そして、(夏至の正午に)シエネにおいて太陽からまっすぐ来る太陽光線の直線を地下の方向に伸ばせば、シエネでは井戸の底から太陽が見える＝まん真上に太陽があるのだから、これも地球中心に達します。また、太陽光線はアレクサンドリアでもシエネでも、(宇宙から見て)平行です。地球よりも太陽の方が大きいのだ、ということを考えれば平行と考えて問題ないとなりますね。以上の事から、図の右上のような作図ができます。図の右上は、図中の地球の図の角張っていないオレンジ色の四角形の部分を拡大したものです。夏至の日の正午に、アレクサンドリアで地面に垂直に立てた棒と太陽光線のなす角度を測定すると、\( 7.2 ^{\circ} \) でした。ということは、図で分かる通り、シエネとアレクサンドリアを結ぶ弧に対する中心角(円周角)も \( 7.2 ^{\circ} \) であるということができますね？あとは、(当時は小学生で習うわけではなかったでしょうが)小学生で習った扇形の知識で地球の周の長さを求めることができます。すなわち、シエネとアレクサンドリアの距離が、当時の測定値で \( 920 km \) だとすると、地球の周の長さを \( L km \) として、小学生で扇形について学んだ通り、\( 7.2 : 360 = 920 : L \) が成り立ち、\( L = 46000 \) が求まります。こうして、地球の周の長さ \( = 46000 km \) が求まりました。実際の地球の周の長さは \( 40000 km \) ですから、 誤差は \( 13 \% \) になります。先にも述べた シエネとアレクサンドリアの正しい距離 \( 800 km \) を用いれば \( L = 40000 \) となりこちらは正確です。また、地球の半径は、\( L = 2\pi r \) の式を用いて求めることができます。円の周が 半径の２倍つまり直径の円周率倍であるという認識は、もっと古代からあったようで、既知としていいでしょう。
さて、地球の大きさがわかると、今度は月食を観察することにより、月の大きさを求めることができます。
月の大きさを求める
エラトステネスは次に、月食を観測することにより、月の大きさも求めることができました。その方法ではそもそもは、地球の直径が月の直径の何個分かが求まるのですが、したがって、地球の直径が具体的にわかっていれば、月の大きさも具体的にわかることになります。この方法は、月食で、太陽に照らされた月が地球の影に入る様子を観測するのですが、月食が太陽に照らされた月が地球の影に入るものであるという事実自体、当時は当たり前の事ではなかったのだから、それを想定して月の大きさを求めてしまった古代人の想像力は、ここでもやはりすばらしいと思います。手の届かないようなはるか天空の上の世界のことを、そんな風に想像できてしまうとは…。
月の大きさの測り方を、まず言葉で説明するとすると、こうなります。月は地球の影のまんなかをつっきるとして(完璧な皆既月食)、月が影に入り始めたとき(瞬間)から、影の中にすっぽり入りきったとき(の瞬間)までの時間を測ります。その時間を \( a \) 分とします。次に、またこの月が影に入り始めたとき、から、月が影から顔を出し始めたときまでの時間を \( b \) 分とします。すると、\( b / a \) は、地球が月の何個分(直径で)の大きさに当たるかを示しているというものです。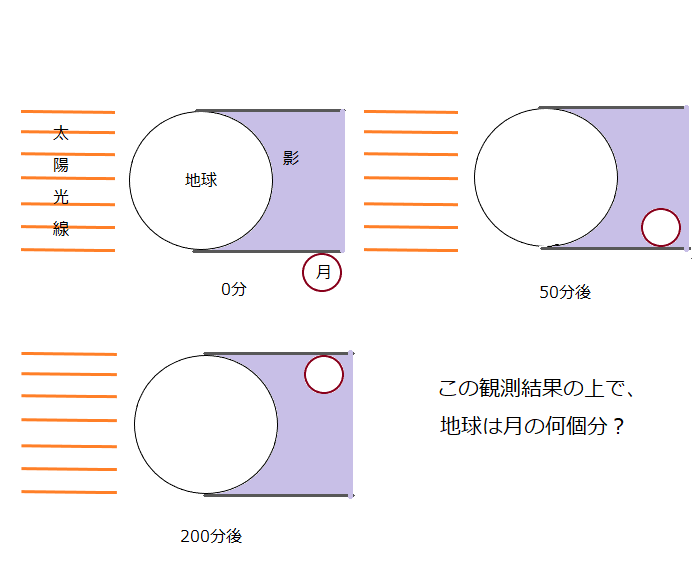
これは、小学校受験や中学校の数学でも出てくる次の問題と同じなので、そちらで解説しましょう。すなわち、「一定速度で走る電車が、ある駅を止まらずに通過するとき、まず、電車の先頭が駅のホームに差し掛かってから、電車の最後尾が駅のホームにすっかり入るまでの時間を \( a \) 秒とします。そして、電車の先頭が駅のホームに差し掛かってから、電車の先頭がホームの一番前の端に達したときまでの時間を、\( b \) 秒とします。駅のホームの長さは、電車の長さ(電車の先頭から最後尾車両の最後尾の長さ)の何個分でしょう？」と、こういう問題です。図を下に示しますが、月の大きさを測ったさっきのやり方は問題はこれと同じです。これはどう求めるかというと、
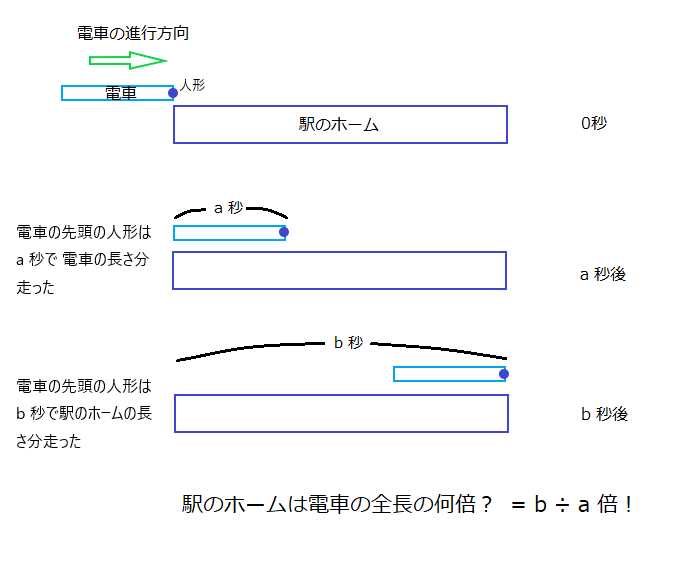
電車の先頭に人形が立っていることにしましょう。電車の長さを \( 120m \) とすると、人形は、\( a \) 秒で、電車の長さ \( 120m \) だけ進みます。また、駅のホームの長さを \( 300m \) とすると、人形は、\( b \) 秒で、ホームの長さの \( 300m \) を進みます。すこしキツネにつままれた感じになるのは、ここではすでに数値が出ているので、駅のホームの長さ \( 300m \) は、電車の長さ \( 120m \) の \( 300 / 120 = 2.5 \) 個分だという答えが自明に出てしまうことですが、\( a \) と \( b \) という値を説明で出したことを考えてください。電車、すなわち人形は一定速度で走っているから、距離でなく時間で計算する \( b / a \) も駅のホームの長さが電車何個分なのかを示しているはずです、すなわち、\( b / a = 2.5 \) です。このようにして、長さを測らなくても、時計を使うだけの方法で電車が駅のホームを通過する様子を観察することにより、駅のホームが電車何個分かがわかります。電車の問題の答えは、\( b / a \) 個分です。
以上で分かったように、地球の大きさも、直径にして月の大きさの \( b / a \) 個分であることが言えるのです。実際の計測によると、月が地球の影に入りきるまで \( 50 \)分、すなわち \( a = 50 \)で、月が影から出始めるまで \( 200 \) 分、\( b = 200 \)なので、地球は直径にして月の \( b / a = 200 / 50 = 4 \) 個分、つまり月の直径は地球の直径の \( 1/4 \) だという結論になります。地球の直径としては、先に求めた地球の周の長さ \( 46000 km \)を用いて計算できる、\( 46000 km / 3.14 = 14650 km \) を使ってみます。地球の直径 \( 14650 km \) に対して、月の直径は \( 14650 \times \frac{1}{4} = 3662 km \) となります。現在のテクノロジーによる精密な月の直径は \( 3474 km \) です。割といい数字が出ています。
こうして、月の大きさを求めることができました。
技巧的で面白い、ハッとさせられるのはここまでで、これ以降はオーソドックスな図形・幾何学の問題になります。
月の大きさがわかると、簡単な観測により、こんどは月までの距離を求めることができます。
月までの距離を求める
今求めた月の大きさを用いて、月までの距離を計算することができます。これは簡単です。
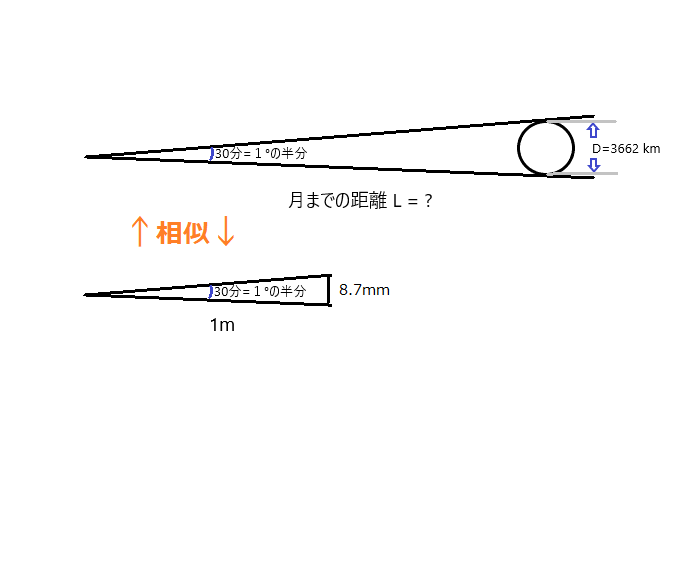
まず、月の視直径を測ります。月の視直径は およそ \( 30 \) 分で、これは \( 1 ^{\circ} \) の半分、すなわち \( 0.5^{\circ} \) です。月までの距離と月の大きさに関して、上図の上の図のように作図することができます。手近なところで、とがった頂点の角度が \( 30 \) 分つまり \( 1 ^{\circ} \) で、側辺の長さが \( 1 m \) の二等辺三角形を作図して描いてみれば(図の下のやつ)、底辺は \( 8.7 mm \) ということがわかるので、三角形の相似を利用して、
\[ 1000 : 8.7 = L : 3662 \]
として、\( L \) を求めることができ、この計算では、\( L = 421000 \) となります。月までの距離が、\( 42 \) 万キロであるという結果を得ました。現在測定されている正しい月までの距離は、月は地球から遠かったり近かったりしますがその平均では、\( 38 \) 万キロなので、いい結果が出ているといえるでしょう。
これは小学校程度の算数の知識によるやり方ですが、高校数学の知識を使うなら、視直径を一応 \( \theta \) で表してみて、\( \theta = 0.5 \times \frac{\pi}{180} \) だから、以下のように、
\[ L\theta = L \times 0.5 \times \frac{\pi}{180} = 3662 \]
となるので、\( L = 420000 \) と求めることもできます。月の直径に当たる部分は正確には弦であり、式は弧に対する式ですが、\( \theta \) が十分小さい時は弦を弧に近似できることを利用しています。
月までの距離がわかると、今度は太陽までの距離を求めることができます。
太陽までの距離を求める。