【天文学】超!高速回転の中性子星
宇宙には中性子性という星があります。自ら輝く恒星のなかで、太陽くらいの重さの星は恒星としての一生の最後に、白色矮星という星になりますが、太陽の8倍~30倍の重さの恒星になると、最後に超新星爆発を起こし、中に残された硬い芯が中性子星になります。もっと重い星は超新星爆発の後にブラックホールになります。
中性子星の直径は10km 程度、回転周期は 1ミリ秒~数秒。
すなわち、直径10km のものが、一秒間に何十回も何百回も回転してるのです!
※直径20km と言っている場合もあります。
宇宙の想像を絶する現象はいろいろあって、想像自体できないくらいすさまじいものも多いですが、中性子星の場合は直径10km なのでこれは身近な長さです。想像はできるけど、想像を絶する高速回転をしている楽しい天体です。
フィギュアスケートの選手が体を細くすると回転が速くなるように、中性子星も、もとの恒星が縮まった結果自転が速くなるのです。
回転がどれだけ速くなるかを計算するには、角運動量保存の法則というものを用います。
角運動量保存の法則というのは、物体に力を加えなかったり、あるいは加えても回転させる力は加えないという場合、角運動量である \( I\omega \) という値が変化しないという法則です。\( I \) は慣性モーメントといって、回転するものの回転にまつわる重みです。例えばひもにボールをつなげて、ぐるぐる円軌道で振り回すとき、その回転しているボールの慣性モーメントは、\( I = mr^2 \) ( \(m\):質量 \( r \):回転半径(ひもの長さ))です。\(\omega \) は角速度です。\( mr^2\) は球形の物体の場合で、物体の “形” によってそれぞれ違いますが、計算で求めることができます。再びいうと、\( I\omega \) が角運動量になります。
太陽くらいの半径で(太陽ではない!)、自転周期が1日である恒星が縮んで中性子星になった場合に自転周期がどれくらい早くなるかを計算してみます。
球体の慣性モーメント \( I \) は、球体の内部の密度が一定だとすると、\( I = \frac{2}{5}MR^2 \) となります。\( M \) は球体の質量、\( R \) は球体の半径です。恒星の内部は密度が一様ではないので正確にはこの値ではありませんが、今回は概算なのでこの \( I = \frac{2}{5} MR^2 \) を用います。
角運動量保存の法則は、
\[ I\omega = \frac{2}{5}MR^2\omega = 一定 \]となります。収縮の際に質量 \(M\) は変わらないと考えれば、これはつまり、\( R^2\omega = 一定 \) ということです。
ところで、\( T \)を星の自転の周期とすると、\( \omega = 2\pi/T \) なので、\[ R^2/T = 一定 \]という結果になります。つまり、恒星が縮んでいく過程で角運動量が保存すると考えれば、その過程の最中は恒星の半径の二乗と自転の周期は比例します。こうして、半径が小さくなれば、つまり星が縮まれば、周期も小さくなる(高速回転)ということがわかりました。
誤解のないように言っておきますが、太陽が中性子星になるのではなく、太陽くらいの半径の星が中性子星になるときの計算をします。(太陽は中性子星よりは大きい白色矮星という星になります)
太陽の半径は\(7\)万km, 中性子星の半径は\(5\)km だから、\( R \) は、星の収縮の際 \( 5km/7万km = 1/14000 \) 倍に縮むことになります。\( R^2 \) はその二乗、\( (1/14000)^2 \) 倍になり、\( R^2 \) と \( T \) が比例するので、\( T \) も \( (1/14000)^2 \) 倍に小さくなります。元の恒星が、”\(1\)日” の周期で自転していたなら、収縮して中性子星になると、周期は \(1\)日\( \times (1/14000)^2 \) になります。これを秒に直すと、\[ 60 \times 60 \times 24 / (14000)^2 = 4.4 \times 10^{-4} 秒 \]
この周期は一秒間におよそ\(2000\)回転に相当します。これは粗い計算で、実際に観測されている中性子星のうち、自転速度の速いものは 一秒間に\(1000\)回転くらいなのですが、ともかく中性子星はこうして高速回転で星ができあがった後、いまはやりの重力波の放出やまだしられていないメカニズムで自転が減速していくものと考えられています。
中性子星の超速の自転速度が角運動量保存によって十分達成可能であることがわかりました。
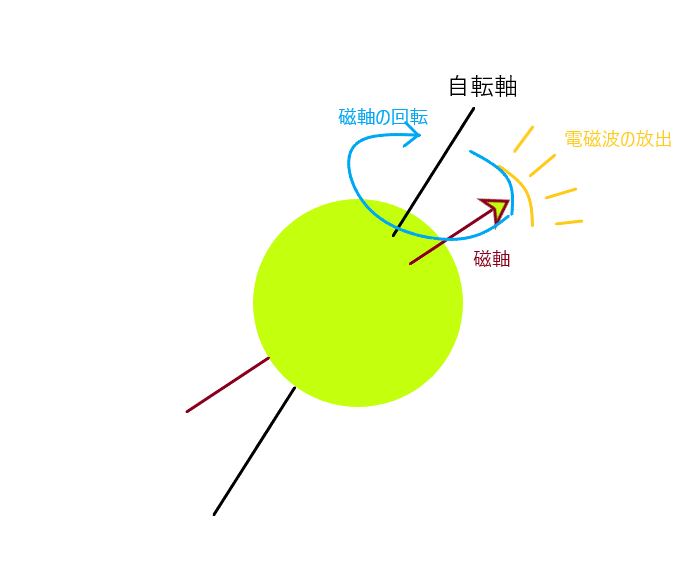
中性子星からは星の磁軸の方向に電磁波が放出されていて、中性子星の回転軸と磁軸が同じでない場合、電磁波の放出される方向がぐるぐる変化することになるので、地球でその電磁波を観測した場合、磁軸が地球の方向を向いたときに強くなるような周期的な電磁パルスとして観測されます。天文学ではまずは望遠鏡が武器で、それで見える現象が研究の入口となるのですが、そのような、周期的に変化する電波を発する天体が発見されたときには、それはパルサーと名づけられました。パルサーは拍動するもの、という意味です。望遠鏡で見ただけではその星が中性子で成り立っていることなどはわかりませんが、他方物理学における中性子の性質に関する研究の過程で、どうやらパルサーは中性子から成り立つ星「中性子星」であるということが、研究の結果しだいに判明していったわけです。
もともとあまりに規則正しいパルスであったため、発見当時は宇宙生命体が発する電波なのではないかとも真剣に考えられたものでした。
そんなに高速で回転していたら、たちまち遠心力で星がまわりに飛び散ってしまいそうに感じられますが、そうなっていないでちゃんと中性子星というカタマリがあるということは、それだけ星の表面の重力が強く、星の物質が中心方向へしっかり引っ張られてるということです。
計算すれば分かる通り、星の表面の重力は密度によって決まる(密度に比例する)ので、これは星の密度が高いことを意味しています。中性子星はものすごくぎゅうぎゅうに固く詰まった星なのです。
表面で物質が吹き飛ばされないためには、どれだけの密度が必要なのかを計算してみましょう。
中性子星の表面での遠心力と重力が等しいとすると、
\[ R\omega^2 = GM/R^2 \]
\(R\) は中性子星の半径、\(M\) は中性子星の質量、 \(\omega\) は中性子星の回転の角速度、\(G\) は万有引力定数です。中性子星の質量は 密度 \(\times\) 体積、つまり
\[ M=\rho \times \frac{4\pi}{3}R^3 \] だから、
\[ R\omega^2 = \frac{4\pi}{3}GR\rho \]
\(R\) が消えて、さらに \(\omega = 2\pi/T\) とすれば、
\[ \rho = \frac{3\pi}{GT^2} \]
一秒に\(1000\)回転、つまり、\(T=10^{-3}\) でも吹き飛ばないわけだから、\(T\) にこれを代入、\( R = 6.67 \times 10^{-11} \) も代入すると、
\[ \rho = \frac{3\times 3.14 \times 10^6}{6.67\times 10^{-11} } \fallingdotseq 1.4 \times 10^{17} [kg/m^3] \]
となります。実際の中性子星の密度は、角砂糖一個(\(1cm^3\)) あたり\(14\)億トンで、これよりちょうど一桁大きい \( 1.4 \times 10^{18} [kg/m^3]\) です。どうして一桁大きい数値が出たのかと言えば、それは、観測されている中性子星は、回転でばらばらになってしまうぎりぎりの状態で回転を保っているわけではなく、それよりも緩い状態で存在しているということです。\(1000\)回転\(/\)秒 の\( \sqrt{10} \fallingdotseq 3 \)倍大きい角速度までばらばらにならない余裕があることになります。回転でばらばらにならないための密度はどれだけか?という今回の計算で、中性子星がいかに高密度でなければならないかは十分説明できたと思います。
もともと中性子星はその発見より前に、統計力学のフェルミ縮退の理論により、超高密度の星が存在するはず、あるいは存在の可能性があるという予測がされていました。中性子星が実際に発見されることにより、理論が裏付けられたのです。
中性子星の核の内部は超流動状態なのではないかとの論もさかんに展開されており、例えば天文学の観測によってそれが裏付けられるようなことがあれば、物理学の理論が発展したりするのです。
このように、物理学と天文学はお互い助け合いながら進歩しています。


ディスカッション
コメント一覧
まだ、コメントがありません