【高校物理】超絶簡単！角運動量保存則の導出
角運動量保存則は、物体に運動方向への外力が加わらない過程で、角運動量：\( mr^2\omega \) が変化しないという法則です。また、例えば太陽の周りをまわる２つの角速度の異なる物体が衝突した場合のように２つ以上の物体がかかわる場合でも、この場合は系に運動方向の外力は作用していない(太陽の重力という中心力のみです)ので、２つの物体の角運動量の合計はやはり保存します。
角運動量保存の法則はエネルギーの考察(エネルギー保存の法則)で導けます。
下図のような状況を考えます。
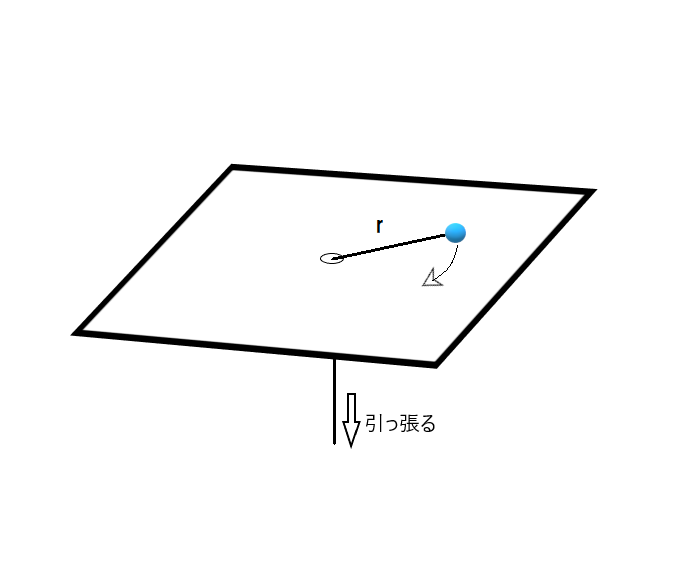
ひもを引っ張っておもりの軌道半径をゆっくり少しだけちいさくしたときのおもりの運動エネルギーの変化を考察します。
下に引っ張る力の大きさは遠心力と同じ大きさです。下に引っ張って動かすには、それよりも大きな力で引っ張らないといけないことになりますが、その大きい分は無視します。仮に、この余分な力が無視できないものであるなら、軌道半径を少しだけ小さく変化させたいだけなのに、中心方向におもりが加速されて動いていってしまい、意図とはことなる運動を招くことになるのです。
簡潔にするため \( m \)を取り除いて考えます。つまり、運動エネルギー \( \frac{1}{2} mv^2 \vartriangleright \frac{1}{2} v^2 \)、 遠心力 \( m \frac{v^2}{r} \vartriangleright \frac{v^2}{r} \)
『(おもりを引っ張って動かしたときの)おもりの運動エネルギーの増分=ひもがした仕事』として運動方程式をたてます。おもりの運動エネルギーの増分は \[ \frac{1}{2}(v+dv)^2-\frac{1}{2}v^2 \] 、ひもがした仕事は遠心力 \( \frac{v^2}{r} \)に距離 \( dr \) をかけて \[ |\frac{v^2}{r} dr| \] となります。ひもを中心方向に引っ張るということは \( r \) が減る、\( dr \) がマイナスであるということを意味することに注意して (つまり、負の \( dr \) に対し、仕事がプラスになるように符号をつける )、また、\( (dv)^2 \) は微少だから無視すると、『おもりの運動エネルギーの増分=ひもがした仕事』を方程式にしたものは以下のようになります。
\[ d( \frac{v^2}{2} ) \color{LimeGreen}{\Bigl( = \frac{1}{2}(v+dv)^2-\frac{1}{2}v^2 \Bigr)} = – \frac{v^2}{r} dr \]
\[ vdv = -\frac{v^2}{r} dr \]
両辺に \( r \) をかけて、
\[ rvdv + v^2dr = 0 \]
両辺を \( v \) で割って、
\begin{equation} rdv + vdr = d(rv) = 0 \end{equation}
角運動量は \( r^2\omega \) ですが、\( r\omega = v \) なので、\( r^2\omega = rv \)
\( (1) \) 式は角運動量 \( rv \) の増分 \( d(rv) \) の満たす式にほかならず、\( d(rv) \) が 0 であることから、ひもを引っ張る過程において \( rv = r^2\omega \) は変化せず、保存されることがわかりました。証明終了。このように角運動量保存の法則は数行の簡単な数式で証明できます！
※ \( (1) \) 式が高校生の知識で分からない場合は、\( dt \) で割って、
\[ r\frac{dv}{dt} + v\frac{dr}{dt} = \frac{d(rv)}{dt} = 0 \] としてください。この式自体が角運動量が保存することを示していますね？