【物理数学】素粒子物理学での群論
SU(2) の 2 ってなぁに?群論はわかったけど物理学とどう関係があるの?などの疑問を念頭に置いての解説。
素粒子物理学で出てくる群論について、かみ砕いて説明します。
まず、群とは。(これは群論の教科書に必ず書かれています)
例えば、整数の集まり(整数全体)と、足し算 + の演算のセットは「群」をなします。整数の集まり(整数全体)と掛け算 \( \times \) のセットも同じく群をなします。
群は、要素(たとえば “整数”)と 演算(たとえば “+”) をセットで群といいます。
要素と演算のセットがあって、それを群と呼ぶには、4つの決まりがあります。これは群の定義です。
①単位元、すなわち、どの要素と演算させても演算の相手を変化させないような要素があること。
②どの要素にも、その要素と演算させると単位元(整数と + の場合なら単位元は \(0\) )になるような対の要素があること。
③要素同士を演算させた結果もやはり要素になること。
④3つの要素を演算するとき、1つめと2つめの演算結果を3つめに演算した結果と、1つめを、2つめと3つめの演算結果に演算した場合が同じものであること(結合の法則)
整数と 演算 + の群であれば、
① \( 1+0=1, 2+0=2…\) のように、\( 0 \) はどの要素に演算(作用)させても、もとの要素を変えないので、\( 0 \) は単位元です。つまり単位元はある。
② 整数には、\( 1 \) に対して \( -1、1.7 \) に対して \( -1.7、2 \) に対して \( -2 \) のように、演算を \( + \) とした場合に作用させると \( 0 \) になる(\( 1+(-1) = 0、2+(-2)=0 \))ような、対(つい)の要素が必ず存在します。( 演算が \( \times \) の場合だと、\( 3 \) に対して \( 1/3 \)、などのように、やはりついが存在して、\( 3 \times 1/3 = 1 \)(単位元) のようにやはり②の条件が満たされます)
③整数同士を足し算すれば整数だから、③も満たします。
④整数の結合の法則は小学生で習いますが、つまり \((1+3)+7 = 1+(3+7)\) で、④の結合の法則も満たします。
※ 群の演算が + の場合だと単位元は \( 0 \) ですが、演算が \( \times \) のような場合だと、単位元は \( 1 \) (や恒等変換) になります。物理で出てくるのはほぼ \( \times \) のような演算の場合で、したがって単位元は \( 1 \) (や恒等変換)になります。
以上のようなことです。でも、物理学への応用が気になります。
正三角形の対称性の群:正三角形の形を変えないような回転操作の変換は、群をなします。え?ってなります。
説明します。
正三角形を時計回りに、120度回転させても形を変えません。120度回転させる操作(変換)を \( r \) とします。240度回転させる操作は \( r \times r (=r^2) \)と表すことができます。この、240度回転させる操作によっても、正三角形は形を変えません。今、群のことを考えていますが、\( r \) や \( r \times r \) は要素に当たります 。演算にあたるものは \( \times \) です。演算 \( \times \) は 変換操作を続けて行うという演算にすぎません。\( a \times b \) は \( b \) に続けて \( a \) を行うという意味です。( 行列を考えればわかるように、\( (a \times b )\times \)[あるベクトル] なら、[あるベクトル]に \( b \) を作用させてからさらに左から \( a \) を作用させるという順序なので、 \( (a \times b) \)という作用は、\( b \) を作用させてから続けて \( a \) を作用させるという順序の作用になります)。物理学での変換の群を考えるときは、”演算”は特に断られることはなく、変換操作を続けて行うという演算 “\( \times \)” が群の演算です。
「変換」が群の要素になっているのです。
正三角形の形を変えない変換として、回転変換のほかにもう一つ、左右反転の変換を考えることができます。この変換を \( f \) とします。\( r \) と \( f \) を合成してできる変換を考え、正三角形の形を変えない変換をすべて挙げると、以下の図のようになります。
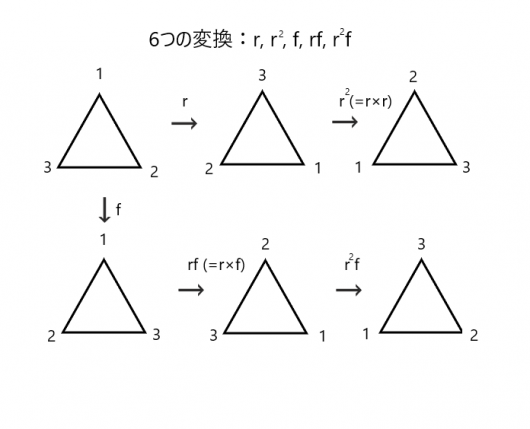
正三角形の頂点に番号を付けてみれば、これら6つの変換が、正三角形の形をかえないながらも別々の変換であることがわかります。また、頂点の番号が同じになるような変換、例えば、\( r^2f \) と \( r^5f \) は同一の変換です。
上記の6つの要素が、 \( \times \) という演算のもと、群としての4つの決まりを満たしていることは、①~④を確認すれば分かると思います。
ちなみに、この群は6つの要素からなる群ですが、要素 \( r \) と \( f \) によってすべての要素を生成することができるので、\( r \) と \( f \) のことを生成子といいます。
あと、整数の群は要素が無限個の群ですが、正三角形対称性の群は有限個の要素の群となります。
以上のことは、つまり、正三角形の形の対称性という自然は、6つの要素からなる群という数学的構造を含んでいるのだ、ということを示しています。正三角形の形は、この変換の群のもと不変であるということです。
素粒子物理学においても同様です。
電磁場において、数式的にゲージ対称性という自然界の対称性を導くことができます。ゲージ対称性とは、電磁場にゲージ変換というものをほどこしても、マクスウェル方程式が形を変えないという対称性です。マクスウェル方程式が形を変えないというのは電磁場が不変だということです。量子論的に考えるとこれは、電磁場内を運動する粒子の波動関数が位相因子 \( e^{i\alpha} \) を除いて変わらないという対称性になります。弱い力や強い力においてもゲージ対称性が発見されているので、電磁場の場合は特に電磁的ゲージ対称性といっておきましょう。
この電磁場のゲージ対称性という自然も、対称性の群を内包しているはずです。
あらかじめ述べておくと、電磁場のゲージ対称性の群は、\( SU(1) \) といいます。
どうして電磁場に群がでてくるの?ということを考えるために、ゲージ変換を施すということを、すこし具体的に掘り下げてみます。
電磁場にゲージ変換 (\( A’=A+\nabla\chi、V’=V-\partial\chi/\partial t \)) を施すと、電磁場内を運動する粒子にたいするシュレディンガー方程式 \[1/2m(-i\nabla-qA)^2+qV)\psi=i\partial\psi/\partial t\] を、その形を変えず成り立たせるようにする、つまり \[1/2m(-i\nabla-qA’)^2+qV’)\psi’=i\partial\psi’/\partial t \] が成り立つようにするためには、\( \psi’ \) を、\( \psi \) と 位相が \( \alpha \) だけ違う \( \psi’ = e^{i\alpha}\psi \) にする必要があることが数式的に示されます。ここで、波動関数にその複素共役をかけることによって得られる粒子の存在確率を計算すると、\( \psi \psi^* \) も \( \psi’ \psi’^* \) も同じになることはわかります。つまり \[ \psi’ \psi’^*= (e^{i\alpha} \psi )(e^{i\alpha}\psi )^* = (e^{i\alpha}\psi)(e^{-i\alpha} \psi^*) = \psi\psi^* \]
シュレディンガー方程式が形を変えない、また、波動関数の表す存在確率も同じであるという、これらの意味で、(電磁場に)ゲージ変換を施しても自然は不変であり、位相が異なる波動関数という、対称性があります。これがゲージ対称性です。
正三角形の時も、頂点の番号は違うけど形が同じであることが対称性であったように、この場合も、位相は違うけど同じ存在確率を表すことが波動関数の対称性です。
そしてつまり、ゲージ変換の結果、波動関数は位相因子 \( e^{i\alpha} \) を作用させられて変換されますが、波動関数は高々位相が変化するだけで、電磁場やその中を運動する粒子の物理は不変なのです。この、波動関数に \( e^{i\alpha} \)を作用させる(かける)変換の集合の全体が、\( \alpha \)を変えれば変換は無限にあることになるので、無限個の要素の群をなしていて、そして、正三角形の対称性の群の場合と同じように考えれば、電磁場(のゲージ対称性)は \( e^{i\alpha} \) の変換の群、すなわち\( SU(1) \)を内包しているということができるのです。これが、電磁場は\( SU(1) \)だ、ということの内容です。この際、何の対称性か細かく言えば、波動関数またはシュレディンガー方程式の対称性ということができますが、それはすなわち、電磁場やその中を運動する粒子の物理が対称であることを示しています。
※ 正三角形の対称性の群で、頂点の番号が違っても正三角形は区別できなかったように、ゲージ対称性の場合も、位相 \( \alpha \) が違っても観測できる存在確率に違いは現れないので、自然を区別できない。頂点の番号に違いが、位相に対応すると考えられます。
場を群で表すのは、場を群で分類するためです。現在、自然界の力の場は、電磁場、弱い力の場、強い力の場、重力場、と4種類であるとされていますが、弱い力の場は \( SU(2) \)、強い力の場は \( SU(3) \)のようになっています。力を統一的に考える統一場の理論でも\( SU(5) \) のような群が扱われます。
■\(SU(…) \) と、\( SU(1) \) の \( 1 \) に関して
波動関数に \( e^{i\alpha} \)をかけることは、複素平面における(波動関数の)回転を意味し、また \( x-y \) 平面内の回転(2次元の回転)とも同じです。2次元の回転は、よく知られているように、変換が作用した結果、作用対象(ベクトル)の大きさを変えず(=ユニタリ:(U)nitairy)、行列式が1 (=特殊:(S)pecial)なので、特殊ユニタリ群:\( SU(1) \) といいます。
\( SU(1) \) の \( 1 \) はとどのつまり電荷が1種類であることに由来します。後述しますがほかの力の場では荷が2種類、3種類でることが発見されています。荷が1種類の場合はゲージ変換の結果、場内の粒子の波動関数は、上でも述べたように2次元回転すなわち、\( SU(1) \) 群の変換を受けます。
荷(弱荷)が2種類である弱い力の場のゲージ対称性は \( SU(2) \) という群で表され, 強い力では、赤青緑の3種類のカラー荷があるから \( SU(3) \) となります。
以上、素粒子物理学における群についてまとめてみました。


ディスカッション
コメント一覧
まだ、コメントがありません