【統計力学】ボース統計・フェルミ統計 の意味
ボース統計とフェルミ統計
ボース統計(ボース・アインシュタイン統計)・フェルミ統計(フェルミ・ディラック統計)と言われても、なにかとてつもなく複雑な背景がありそうな感じがします。そして、何の統計なんだかわからない。
「統計」というのは、あの統計ですよね?数学で習う、「統計」です。統計を教える教科書があってそれだけ膨大な内容があり、統計という言葉が示すものの幅が広すぎるから、ボース統計・フェルミ統計と言われてなにか圧倒される気がする。
実際には、ボース統計・フェルミ統計は、ボース分布・フェルミ分布と同じです。とても狭い意味です。
ボース統計・フェルミ統計とは簡単に言うと、温度 \( T \) の環境の中でボース粒子やフェルミ粒子が “エネルギー的に” どう分布するかの統計で、番号 \( r \) の量子状態、つまりエネルギー \( \varepsilon_r \) の状態をとる粒子がいくつになるのかの数(の期待値)を求めた結果です。
例えば、正規分布も、「自然的な」要素の集団にたいする統計です。同様に、ボース統計・フェルミ統計も、(統計力学の) 「グランドカノニカルな」粒子の集団にたいする統計です。この統計を用いて粒子のエネルギーにたいする粒子数の分布を求めたものが、ボース分布・フェルミ分布です。グランドカノニカル集団の統計法というのは、\( N \) 個の粒子の系において、各エネルギー状態 \( (\varepsilon_0, \varepsilon_1, \varepsilon_2, \varepsilon_3, … ) \)を占める粒子数が \( ( n_0, n_1, n_2, n_3, … ) \) である確率が
\[ P(n_0, n_1, n_2, n_3, … ) = \frac{1}{\Xi(T, \mu )} exp[-\frac{1}{k_B T}\Sigma_i(\varepsilon_i – \mu)n_i ] \]
であるという結果を用います。
\[ \biggl( P(N, E_n) = \frac{1}{\Xi(T, \mu) } exp[-\frac{1}{k_B T}(E_n – \mu N) ] \biggr) \] (本当はグランドカノニカル分布といったらこちらで、その上の式はこの式に少し代入したもの:また、式中 \( exp[-\frac{1}{k_B T}(E_n – \mu N) ] \) が確率を意味するのであるが、それは相対確率の身分で、したがって全確率を \( 1 \) に規格化するために、相対確率のすべての和として定義される大分配関数 \( = \Xi(T, \mu) \) で割っている。\( \Xi \) = クシー
統計というからには多数の粒子があるから統計を考える意味があるわけです。そして、ボース分布・フェルミ分布というのは、多数のボース粒子またはフェルミ粒子の集団があったとき、その中で「エネルギーEをとる粒子」がいくつあるのか、つまり、エネルギーEに対して、そのエネルギーをもつ粒子がいくつになるのか、の分布です。(正確には、古典統計であれば、エネルギー \( E \sim \Delta E \) の範囲の粒子がいくつなのかの分布、ということになるし、量子統計であれば、エネルギーが \( E_n \) の粒子がいくつなのかの分布、ということにはなります)
金属内の自由電子に対してはフェルミ分布を用いることができます。ヘリウム 4He はボース粒子で、ボース分布が適用でき、極低温の 4He が超流動状態(ボースアイン主体凝縮)を示すことがわかります。
上述の手法で得られる実際の結果は以下のようになります。すなわち、\( n_r \) を、\( r \) 番目の状態を占める粒子の数とし、あるいはこれはずばりエネルギーが \( \varepsilon_r \) の状態の粒子の数ですが、そして、\( <n_r> \) を \( r \) 番目の量子状態をとる粒子数の期待値(つまりエネルギー \( \varepsilon_r \) をとる粒子の個数の期待値)とすると、
\( <n_r>= \frac{1}{e^{(\varepsilon_r -\mu)/k_B T} – 1 } \ \ \ \ \ \dots \text{ボース粒子} \)
\( <n_r>= \frac{1}{e^{(\varepsilon_r -\mu)/k_B T} + 1 } \ \ \ \ \ \dots \text{フェルミ粒子} \)
となります。
後述しますが、これら二つの導き方は、同じ手順に従います。手順の中で、同じエネルギーに何個でも粒子が入れるボース粒子の場合は ある \( i \) にたいし \( n_i = 0, 1, 2, 3, … \infty \) とするのに対して、同じエネルギーに一つしか粒子が入れないフェルミ粒子は \( n_i = 0 \ or \ 1\) とするだけの違いがあるだけなので、両者の表式は見た目が非常に似たようなものになっています。
以下では、全エネルギーは離散的であると考え、\( E \) は \( E_n \) などに置き換わります。
粒子の統計を調べる、とはどういうことかというと、それは、熱浴内にある閉じた系または開いた系の粒子の統計を調べる(た)ということです。粒子の統計といっても、まず調べて最初に得られるのは粒子の作るその系の全エネルギー \( E \) がとる値の確率分布 \( P(E) \) です。
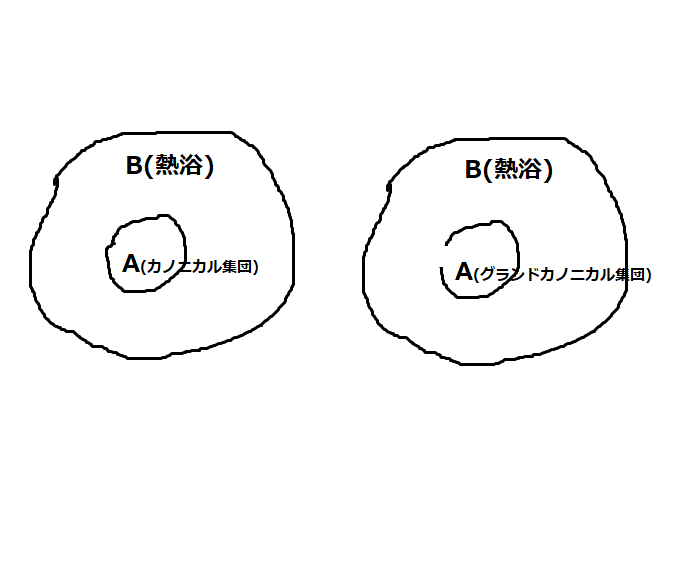
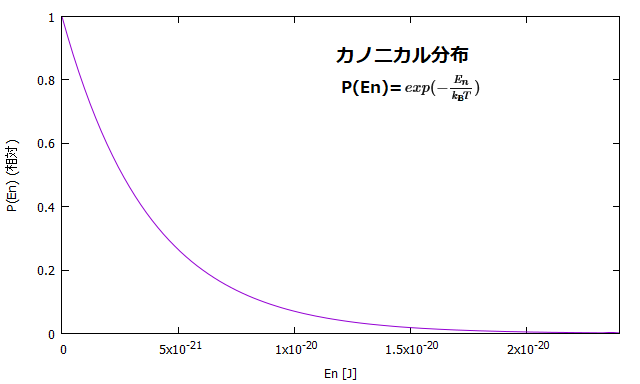
カノニカル分布とグランドカノニカル分布
それではその、全エネルギー \( E \) がとる値の確率分布 \( P(E) \) はどうやって得たかというと、閉じたまたは開いた系を含む熱浴の全体をミクロカノニカル集団として扱い、ボルツマンの原理とエントロピーを用いることで計算できます。結果は、閉じた系の場合のエネルギーの確率分布は \( P(E_n)= \frac{exp(-\frac{E_n}{k_B T} )}{\Sigma^\infty_{i=0} exp(-\frac{E_i}{k_B T}) } \) となり、この分布確率 \( P(E_n) \)で表されるような分布をカノニカル分布といい、このエネルギーの確率分布をしめすこの閉じた系の集団を、カノニカル集団といいます。開いた系のほうは、\( P( N, E_n) = \frac{exp[-\frac{1}{k_B T}(E_n – \mu N )] }{\Sigma_i exp[-\frac{1}{k_B T}(E_i – \mu N )]} \) となり、この確率分布はグランドカノニカル分布と呼ばれます。こちらの集団はグランドカノニカル集団といいます。ボース統計・フェルミ統計を導くのに使うのはこちらのグランドカノニカル分布です。ボース統計・フェルミ統計の対象となる粒子の集団を、グランドカノニカル集団と見るからです。

みけ
カノニカル分布とグランドカノニカル分布はそのような関係となっています。
この際閉じたまたは開いた系の全粒子数を \( N \) としますが、この \( N \) 粒子系における、各量子状態を占める粒子数が \( ( n_0, n_1, n_2 … ) \) である確率が、
\( P(n_0, n_1, n_2, …) = P(\{ n_i \}) = \frac{1}{\Xi( T, \mu)} exp( – \frac{1}{k_B T} \Sigma_i (\varepsilon_i – \mu) n_i ) \)
であることを求めてから、それを用いると、今度は全エネルギーでなく一つの粒子のエネルギーに焦点を当てた統計つまり、エネルギーが \( \varepsilon_n \) である粒子がいくつあるか(エネルギーが \( \varepsilon_n \) の粒子の個数の平均値)を得ることができます。それこそがボース分布とフェルミ分布です。これでようやく統計という統計らしくなりました。カノニカル分布の前段の部分だけでは、これを統計的なことだといっても僕はいまいち納得しませんが、このように粒子一つに着目できて、粒子のエネルギーの値に対する粒子数分布がわかるのであれば、それは間違いなく統計であるということができると思います。カノニカル集団やグランドカノニカル集団とは統計的に言ってそのような確率分布で示される粒子分布を呈する集団なのだ、と。
黒体輻射ででてくる空洞内の電磁波(光子の集まり)はカノニカル集団で、空洞の温度を \( T \) とすれば、電磁波のエネルギーのとる値の分布はカノニカル分布のそのまま \( P(E_n)= \frac{exp(-\frac{E_n}{k_B T} )}{\Sigma^\infty_{i=0} exp(-\frac{E_i}{k_B T}) } \) です。角振動数 \( \omega \)を固定して考えると、1つの光子はエネルギーが \( \hbar\omega \) で、光子が \( n \) 個あるとすれば電磁波の全エネルギーは \( E_n = n \hbar\omega \) 。この \( E_n \) をそのまま \( P(E_n ) \) に適用したものを使って(角振動数が \( \omega \)である)電磁波のエネルギーの期待値を計算することができます。光子はカノニカル集団としてもともと考えていたような閉じた系のなかの物質の粒子とはなんとなく描像が違う気がしますが、光子は紛れもなく粒子であるし、また、光子が熱浴に移動することによってエネルギーを持ち逃げすることがないので、グランドカノニカル集団でなく、カノニカル集団として扱うことができます。カノニカル集団とグランドカノニカル集団の違いの本質は、グランドカノニカル集団では、粒子が壁の外と自由に行き来でき、その際エネルギーを持ち去ったり持ち込んだりしてしまうという点です。
また、金属内の自由電子は、グランドカノニカル分布を少しばかり応用しただけで得られる結果であるフェルミ分布を示します。フェルミ分布は半導体の計算や、超高密度状態で現れる反発力である縮退圧の理論などへ応用が利きます。超流動のボース・アインシュタイン凝縮はまた、ボース統計の理論から得られる発展的内容です。
ボース統計とフェルミ統計の違い
ボース統計とフェルミ統計の違いは、ボース統計はボース粒子に対する統計であり、フェルミ統計はフェルミ粒子のものであるという点につきますが、それを導く際の違いは、以下の点にあります。
まず、ボース粒子の場合もフェルミの場合も、粒子の集団は熱浴内の開いた系であるグランドカノニカル集団として扱い、グランドカノニカル分布を使用します。
そのうえで、ボース統計かフェルミ統計かの違いは、全状態の和の計算の際に、エネルギー \( E_i \) をとる粒子の数 \( n_i \) を、\( n_i = 0, 1, 2, …\infty \) 、にするのか、\( n_i = 0, 1 \)にするか;つまり \( 0 \) または \( 1 \) のみに限定するのかの違いで、前者は粒子数に対する条件として特に制約もなく分布を導く方法ということができ、それがボース統計の方法です。後者は、分布を導く際に 1つの状態(ここではエネルギー状態)に2つ以上の粒子が入れないという、フェルミ粒子に対するパウリの排他率の制約を課したかたちになっており、これがフェルミ統計の方法です。フェルミ統計に従う粒子をフェルミ粒子と言う、わけではなく、フェルミ粒子の性質が反映されて、フェルミ統計が導かれる、というのが妥当です。
フェルミ統計とは何かと聞かれたら結局答えは、熱浴内にある、粒子が熱浴と出入りできる開いた系内の”フェルミ”粒子の統計であり、その系はグランドカノニカル集団です。またそれは、グランドカノニカル集団を扱う方法をそのまま適用して計算した、粒子のエネルギーに対する個数分布で、ただ計算の際にフェルミ粒子の決まりであるパウリの排他率を加味したもの、であるということができます。この系の例を具体例に求めれば、この熱浴内にある粒子の出入りできる開いた系というのは、すなわち金属内の自由電子の系のモデルであるという言い方ができるでしょう。金属内の自由電子はフェルミ統計で扱えます。そして、上記でパウリの排他率を考慮しなければそれはボース分布です。
統計力学の基礎 ~統計に従う
正規分布は、ある集団があり、例えばテストの点数の統計を取った場合、平均点をとる人が一番多くて、そこから低くも高くも、点数が平均から離れた人の人数が少なくなる、そしてその分布の様子が、正規分布で示されるような分布を示す、という分布です。自然のものの分布というのは、たいてい正規分布に従っています。
統計力学では熱浴内の、壁に囲まれた中の粒子の集団を扱うのですが、テストの点数の代わりに、粒子(一つの粒子のこと)のエネルギーの大きさを考えます。物理学でよく知られているように、エネルギーの低い状態は安定で、高いエネルギーの状態ほど、エントロピーがエネルギーの変化に敏感になり \( ( \partial S/\partial E = \) 大 \( ) \) 、実現しがたい状態であり、粒子数が少ない。テストの点数の場合と粒子のエネルギーの場合は異なり、粒子の場合は、壁によりエネルギーの分配が行われ、エネルギーが低いほど得やすい状態であり正規分布にはならず、物理を考えた統計が必要になってくるわけです。具体的にはボルツマンの原理、エントロピーの考察からエネルギーの分布が導かれます。
再び結果だけを示せば、エネルギー \( \varepsilon_r \) の状態をとる粒子数(の平均値)は、
\( <n_r>= \frac{1}{e^{(\varepsilon_r -\mu)/k_B T} – 1 } \ \ \ \ \ \dots \text{ボース粒子} \)
\( <n_r>= \frac{1}{e^{(\varepsilon_r -\mu)/k_B T} + 1 } \ \ \ \ \ \dots \text{フェルミ粒子} \)
となります。これが、ボース分布とフェルミ分布です。ボース統計・フェルミ統計という統計法をとったうえでの統計的な結果ということです。
重複しますが、ボース分布あるいはフェルミ分布、すなわち、エネルギー \( \varepsilon \)をとる粒子の個数(個数分布)を導くときの考え方は、各エネルギー状態を \( (\varepsilon_0, \varepsilon_1, \varepsilon_2, …) \) とし、それを占める粒子数が \( (n_0, n_1, n_2, …) \) である確率 \( P( n_0, n_1, n_2, …) \) が、\( P( n_0, n_1, n_2, …) = \frac{1}{\Xi( T, \mu)} exp( – \frac{1}{k_B T} \Sigma_i (\varepsilon_i – \mu) n_i ) \) であるということから、それを利用して( \( \varepsilon_r \) をとる粒子の数のすべての場合を足し合わせるようにして )、エネルギー\( \varepsilon_r \)をとる粒子の個数の期待値を求めるということです。この計算がきになる場合は、「講談社 基礎物理学シリーズ 8 統計力学」を参考にしてください。
ボース粒子やフェルミ粒子は、それ以前に知られていた統計と違う、このような統計に従う粒子であるということができるのです。
また、ボース分布やフェルミ分布を導くには、系をグランドカノニカル集団として扱い、グランドカノニカル集団を扱う方法でエネルギーvs粒子数の分布を求めますが、グランドカノニカル集団はカノニカル集団の応用です。そのカノニカル集団の方法を見てみます。熱浴の中にあって、粒子数が変化せず熱浴とエネルギーの授受のみがある系はカノニカル集団です。この集団が全体としてエネルギー \( E_n \) を取る確率は
\[ P(E_n) = \frac{exp[-\frac{E_n}{k_B T}]}{\Sigma_i exp[-\frac{E_i}{k_B T}]} \]
で表されます。この式から、エネルギーが高いほどそういうエネルギーをとる確率が低いことがわかると思います。一方、グランドカノニカル集団とは、カノニカル集団の、さらに熱浴と粒子の行き来がある集団です。
グランドカノニカル集団では、熱浴の中の系 \( A \) が粒子数 \( N \)、全エネルギー \( E_n \) をとる確率は、
\[ P_A( N, E_n) = \frac{exp[-\frac{1}{k_B T}(E_n – \mu N )] }{\Sigma_i exp[-\frac{1}{k_B T}(E_i – \mu N )]} \]
となります。ボース分布・フェルミ分布を計算するときは、\( E_n \to \varepsilon_r \) のようにしました。ボース分布・フェルミ分布を導く際になぜカノニカル集団でなく粒子の行き来することを許すグランドカノニカル集団として扱わないといけないかは、ボース分布・フェルミ分布で扱う粒子集団は、例えば自由電子の集団であっても、原子から電子が飛び出たり原子の中に電子が吸い込まれたりするし電子が周りにエネルギーを持ち去ったりする状況があるから当然なのですが、それでもカノニカル分布とグランドカノニカル分布の式は基本的には似ていて、カノニカル分布を用いてボース分布・フェルミ分布を計算しても、なにか似たような結果の式が導かれるはずだと思います。
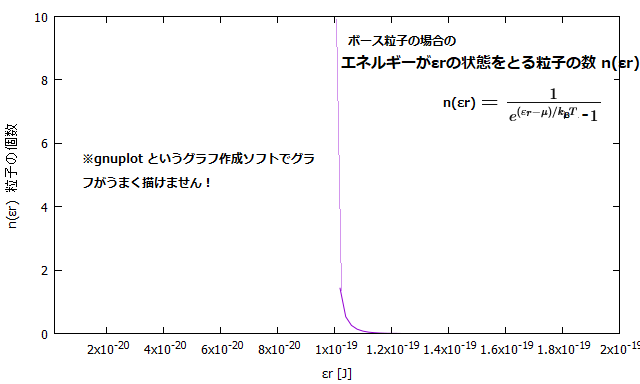
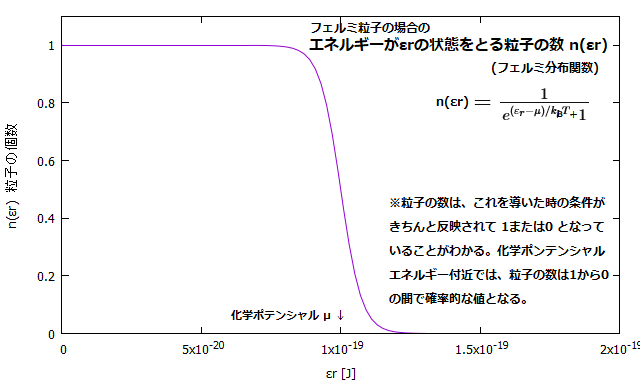


ディスカッション
コメント一覧
ボース統計とフェルミ統計の分布関数の表式が逆になってますよ。
ご指摘ありがとうございます。さっそく訂正させていただきました。これからも応援よろしくお願いします。