【天文学】太陽の高度が低いと地面が暖められないわけ
高緯度ほど太陽の高度が低く、寒い=気温が低いのはなぜかというよくある疑問です。
ここでは正確な理解に重点を置いて説明します。
光は波動でもあり粒子でもありますが、ここでは光の粒子性を考えればいいのです。つまり光はつぶつぶです。ボール球と考えてもいいでしょう。
一秒間に一平方メートル当たり垂直に10000個の光の粒が貫いているとします。
この光が仮に地面に”垂直”に当たれば、一秒間に一平方メートルあたり10000個の粒がぶつかりますが、角度が垂直より浅くあたれば、10000個が一平方メートルより広がった範囲に広がって着地するので、”一平方メートルあたり”にぶつかる粒は減ります。地面一平方メートルあたりに到達する粒は、角度が浅いほど少なくなるので、それだけ地面が刺激されないことになり、温度もあがりません。これが高緯度で気温があがらない根本的な理由です。
太陽の高度(角度)を \( h \) とすると、一秒間に一平方メートルあたりの面に垂直に10000個の粒が貫く流れは、地面では \( 1/\sin h \) 倍の面積に広がるので、地面一平方メートルあたりにぶつかる粒の数は、\( 10000 \times 1/(1/\sin h) \) = \( 10000\sin h \) 個と計算できます。つまり粒の数は垂直に貫く場合の \( \sin h \) 倍になります。
光強度とはもともと光がその進行方向に垂直な面\(1m^2\)を\(1\)秒間に貫くエネルギーで定義されますが、
単純に、エネルギーは粒の数に比例すると考えていいので、もともとの粒の流れ、光強度が \( I [J/(m^2\cdot s)] \) だったとすると、高さ(の角度) \( h \) から入射した光の地面での強度は、\( I \sin h [J/(m^2\cdot s)] \) となります。
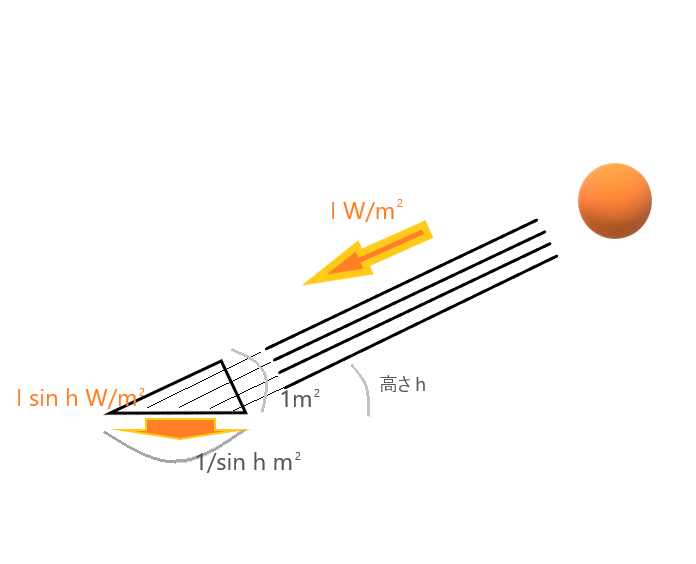
( \( W/m^2 = J/(m^2\cdot s) \) )
太陽の高度 \( h \) が \( 60^{\circ} \) であった場合、\( \sin h \) は \(1/2\)だから、つまり地面では光の束は2倍の面積にひろがり強度は半分(\(1/2\))になります。


ディスカッション
コメント一覧
まだ、コメントがありません