【気象・熱力学】気温が一番高い時刻が正午より遅れるわけ
一日の気温が最高になるのは、太陽が一番高い昼の12時ではなく、午後の2時や3時です。太陽が一番高い時に最高気温になる気もしますが、そうならず遅れるのはなぜでしょう?
これは、簡単に言うと、太陽が一番高いときでも、まだ、「地面が太陽から受け取る熱=受けとる熱」のほうが、「地面が放射する熱=放射する熱」よりも大きい状態であるため、正味の受け取る熱のために、温度が上がり続けているからです。やがて、受けとる熱が減り、放出される熱と等しくなったときに最高気温を迎え、放出される熱が受け取る熱を上回り始めると、温度が下がり始めます。
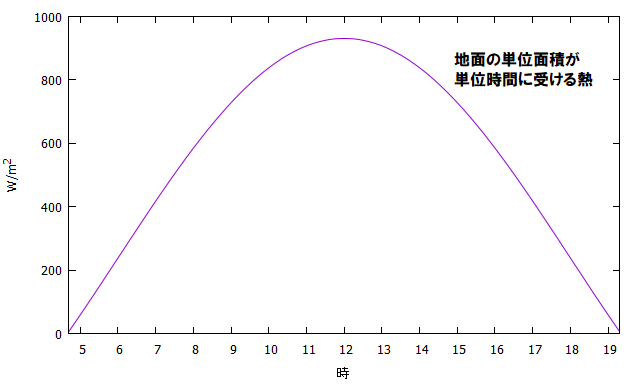
(単位面積当たりの)地面が太陽から受ける熱はグラフのように変化します。(単位面積当たりの)地面が受け取る熱がこのように変化するのは、まず太陽放射自体は一定と考えていいのですが、(単位面積当たりの)地面が受ける熱が太陽の高度、つまり太陽光線と地面のなす角度によって変化することによります。
グラフ(理論値) \( 950\times\sin(h) = 950\times(0.25 + 0.73\cos(15T-180)) \)
図
以下、熱とエネルギーは同じ意味です。熱はエネルギーです。(エネルギーは熱だけに限らず非常に様々ですが、熱は種類あるエネルギーのうちの一つすなわち、熱エネルギーです)
太陽光線に垂直な面の単位面積あたりに含まれる太陽放射は、地面にそそぐときに \( 1/\sin(h) \) 倍(\(h\):太陽高度)の面積に広がって薄められてしまうため、地面の単位面積当たりに届くエネルギーはその \( 1/(1/\sin(h) ) \) = \( \sin(h) \) 倍になります。\( \sin(h) \) は、\( \sin(h) = \sin(\varphi)\sin(\delta) + \cos(\varphi)\cos(\delta)\cos(t) \) のようにあらわされます。( \(\varphi \), \(\delta \), \(t\) については後述。)
※ここでは地面が太陽から受け取るエネルギーを計算で求めていますが、実際に地表が受けとるエネルギーを観測したデータがあれば、以下の \( E \) をそれに代えて同様に考えることができます。
地面に届くエネルギーはすべてが吸収されるわけではなく一部が反射されるためその吸収率を加味し、\(1m^2\)の地面が\(1\)秒間に太陽から受け取るエネルギーは \( E \) =全天日射(およそ1000W)×吸収率(0.95程度)× \( \sin(h) \) となります。また、\(1m^2\)の地面から\(1\)秒間に地面から逃げていく(放射される)熱はシュテファン=ボルツマンの法則より、シュテファン=ボルツマン定数 \( \sigma \) を用いて \( \sigma T^4 \) と表されます。\( E \) と \( \sigma T^4 \) が等しくなった時が地面が受け取る熱と放射する熱が等しくなる時です。このとき、\( T \) が一日のうちで最高の状態にあることになります。なぜなら、これ以降は、\( \sigma T^4 \) のほうが \( E \) よりも大きくなる、すなわち 放出\( > \)受け取り という状況になるため、それまで上昇していた温度 \( T \) が下がり始めるからです。
グラフ
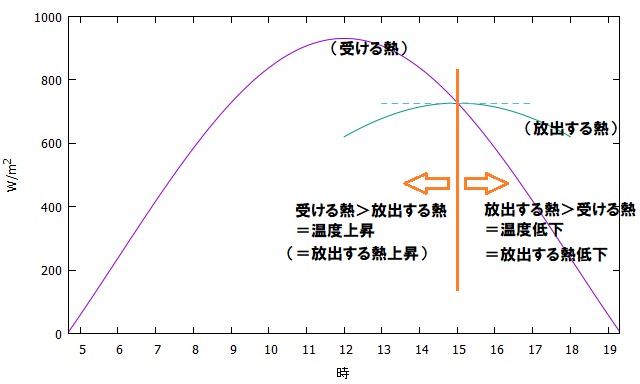
図で説明すると、\( \sin(h) \) と \( \sigma T^4 \) が交わるところで \( \sigma T^4 \) が頂点、つまり最大となっているようなグラフになります。\( \sigma T^4 \) が最大ということは、\( T \) も最大ということを意味しますから、一日の最高気温はこうして、昼の12時からおくれることになるのです。図には放射する熱としか描かれていませんが、温度(気温)も放射する熱と同じようば変化の様子をを示します、すなわち、放出する熱が最大の時気温も最大となります。
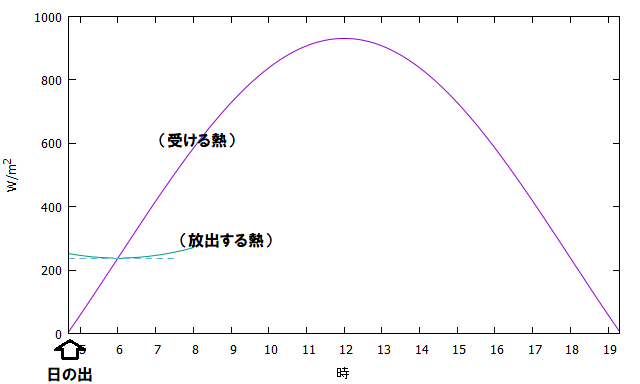
朝についても同様に考察すると、日が出たばかりの時間では気温は上昇せず、しばらく気温の低下が続いたのちに気温があがりはじめることがわかります。日が出たばかりの地面ではまだ地面から放出される熱(エネルギー)のほうが、地面が太陽から受けるエネルギーを上回っており温度は低下していくままで、太陽の高度が増し地面が受け取るエネルギーが放出されるエネルギーを上回りはじめると、気温の低下がとまり上昇に転じます。
グラフ
これらのことについて、微分方程式を書いてみましょう。この微分方程式を、コンピューターシミュレーションで解くこともできます。
\( 太陽高度 h = \arcsin(\color{Green}{\sin(\varphi)\sin(\delta) + \cos(\varphi)\cos(\delta)\cos(time)}) \)
\( \sin(h) = \color{Green}{\sin(\varphi)\sin(\delta) + \cos(\varphi)\cos(\delta)\cos(time)} \)
定義:\( time = 15t_h – 180 \) たとえば ( \(t_h\) の \( h \) は hour の意味=時刻[1時、2時、3時…] \( t_h=12 \) つまり\(12\)時で \(time=0\) となります。)
\( \varphi \):北緯、\( \delta \) :太陽赤緯 ±23°27′ の間。本記事の説明の計算では夏至の場合の +23°27′ を使用。
簡略化して、\( \sin(h) = A+B\cos(15t_h-180) \) としておきます。
・地面が受ける熱(単位面積、単位時間):
\( X= \) 全天日射(1000W) \( \times \) 地面吸収率(0.95) \( \times \sin(h) \) = \( F \sin(h) = F(A+B\cos(15t_h-180)) [J/(m^2\cdot s) ]\)
・地面が放出する熱(単位面積、単位時間):
\( Y=\sigma T^4 [J/(m^2\cdot s)] \)
\( C \) を熱容量とし、正味の吸収エネルギーが地面を温める方程式は次のように書けます。
\[ C \frac{dT}{dt} = X-Y = F(A+B\cos(15t_h-180)) – \sigma T^4 \]
\( = F(A+B\cos(15t/3600-180)) – \sigma T^4 \) (\( t \) :時刻の秒表示)
\( = F(A+B\cos(t/240-180)) – \sigma T^4 \)
\( = F(A+B\cos \pi(t/43200-1) ) – \sigma T^4 \) (=radian 表記)
\[ \therefore C \frac{dT}{dt} = F(A+B\cos \pi(t/43200-1) ) – \sigma T^4 \]
ただし \( F = \) 全天日射\((W)\) \( \times \) 地面吸収率 \( (0<r<1) \)
\( A=\sin(\varphi)\sin(\delta) \)、\( B=\cos(\varphi)\cos(\delta) \)、\( C: \) 地面の単位面積に当たる部分の熱容量、これは実験的に求めたほうがいいかなぁ~~。要は地面一平方メートルを一度上げるの必要な熱量。深さ方向の問題があって、熱伝導を考えなくてはいけない。
全天日射と地面吸収率を変えてコンピューターシミュレーションしてみてもいいかもしれません。
※本記事では熱とエネルギーが混在して使われていますが、本記事の文脈においては熱とエネルギーは言い換えても同じです。ただしほんとうは、熱は、熱エネルギーというエネルギーですが、エネルギーは熱エネルギーのほかに、運動エネルギーや位置エネルギー、静電エネルギーなどさまざまな形があり、エネルギーは熱に限られません。


ディスカッション
コメント一覧
まだ、コメントがありません